Будем рассматривать следующую задачу:
Пусть имеется СВ 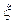 для которой плотность распределения
для которой плотность распределения 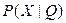 известна с точностью до
известна с точностью до 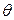 . Например:
. Например: 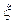 - распределено по нормальному закону:
- распределено по нормальному закону: 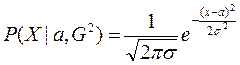 ,
, 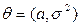 .
.
Требуется оценить параметр 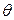 . Для решения этой задачи с помощью независимых опытов получим значения СВ
. Для решения этой задачи с помощью независимых опытов получим значения СВ 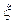 . С помощью математических методов находят оценку неизвестного параметра. Совокупность опытных данных:
. С помощью математических методов находят оценку неизвестного параметра. Совокупность опытных данных: 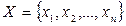 называется выборкой.
называется выборкой. 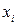 - значение величины в i-ом опыте где
- значение величины в i-ом опыте где 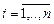 и
и 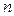 - объём выборки.
- объём выборки.
Тогда оценка 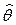 неизвестного параметра
неизвестного параметра 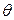 есть функция опытных данных:
есть функция опытных данных: 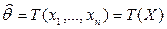 .
.
Задача теории оценок указания вида функции 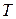 .
.
Определение: Если математическое ожидание оценок равно истинному значению параметра, то оценок называется несмещённой, т.е. 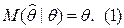 .
.
Величина 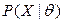 равна плотности распределения вероятности выборки X.
равна плотности распределения вероятности выборки X. 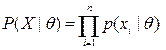 (условие несмещённости)
(условие несмещённости) 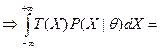
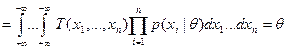 . Примем условное обозначение:
. Примем условное обозначение: 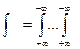 .
.
Определение: Если соотношение (1) не выполняется, то оценка называется смещённой, а величина 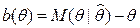 называется смещением.
называется смещением.
Определение: Если имеет место условие: 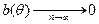 , то
, то 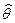 называется асимптотически смещённым. В качестве меры точности оценки берётся её вариация, т.е. среднее значение квадрата разности между оценкой и неизменным значением параметра:
называется асимптотически смещённым. В качестве меры точности оценки берётся её вариация, т.е. среднее значение квадрата разности между оценкой и неизменным значением параметра: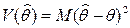 или последнее равенство переписывается в виде:
или последнее равенство переписывается в виде: 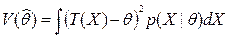 .
.
Рассмотрим свойства вариации:
1. 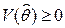 .
.
2. Если оценка не смещённая, то вариация оценки равна её дисперсии: 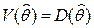 .
.
 2014-02-02
2014-02-02 1472
1472








