Определение: Генеральной совокупностью называется совокупность объектов или наблюдений, все элементы которой подлежат изучению, при статистическом анализе.
Понятие генеральной совокупности аналогична понятию случайной величины.
Генеральная совокупность может быть конечной иди бесконечной.
Определение: Объектом генеральной совокупности называется число её объектов или наблюдений.
Определение: Выборочной совокупностью или выборкой называется часть объектов генеральной совокупности использованной для исследования.
Сущность выборочного метода в математической статистике заключается в том, что бы по определению части генеральной совокупности выборки судить о её свойствах в целом. Для того, что бы по выборке можно было судить о генеральной совокупности выборка должна быть репрезентативной.
Определение: Репрезентативная выборка обеспечивается случаем отбора её элементов, т. к. все элементы генеральной совокупности должны иметь одинаковую вероятность попадания в выборку.
Имеется 2 способа образования выборки:
1) повторная выборка (когда каждый элемент случайно обобранный и исследованный возвращается в общую совокупность и может быть отобран повторно);
2) бесповторная выборка (когда отобранный элемент не возвращается в общую совокупность).
Пусть некоторые признаки описания некоторой СВ X. Рассмотрим выборку 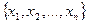 объёма n из генеральной совокупности. Элементы этой выборки представляют собой значения СВ X. На первом этапе производится ранжирование выборки, т.е.
объёма n из генеральной совокупности. Элементы этой выборки представляют собой значения СВ X. На первом этапе производится ранжирование выборки, т.е. 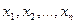 , упорядочены по возрастанию.
, упорядочены по возрастанию.
Определение: Вариантами 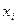 называются различные элементы выборки.
называются различные элементы выборки.
Определение: Частотой варианты 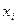 называется число
называется число 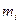 , показывающая сколько раз варианта
, показывающая сколько раз варианта 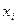 встречается в выборке.
встречается в выборке.
Определение: Относительной частотой варианты 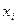 называется
называется 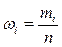 .
.
Определение: Пусть x – некоторое число, тогда, количество вариант 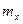 , значение которой < x называется накопленной частотой
, значение которой < x называется накопленной частотой 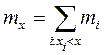 .
.
Определение: Относительной накопленной частотой называется 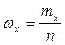 .
.
Определение: Вариационным рядом называется ряд вариант расположенных в порядке возрастания с соответственными частотами и относительными частотами.
Вариационный ряды бывают дискретные и интервальные.
Определение: Дискретным вариационным рядом называется ряд, который представляет собой выборку значений дискретной СВ.
Общий вид вариационного ряда:
| Варианты: | x1 | X2 | … | xk |
| Частоты: | m1 | M2 | … | mk |
Определение: Интервальным вариационным рядом называется ряд, который представляет собой выборку значений СВ.
Построенный интервал вариационного ряда можно разбить на полуинтервалы вида 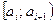 , т.е. произвести из группировку. Количество интервалов k рекомендовано выбирать по формуле Стерджеса:
, т.е. произвести из группировку. Количество интервалов k рекомендовано выбирать по формуле Стерджеса: 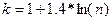 . Длина каждого интервала
. Длина каждого интервала 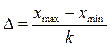 .
.
Подсчитывая количество значений попавших в каждый полуинтервал 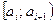 получаем значение
получаем значение 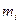 :
:
| Варианты: | 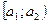 | 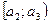 | … | 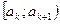 |
| Частоты: | m1 | m2 | … | mk |
Для наглядности представления дискретного и вариационного ряда используются графические представления:
- Полигоны.
- Гистограммы.
- Камулянты.
Полигон служит для изображения дискретного вариационного ряда и представляет собой ломаную соединяющую точку с координатой 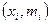 ,
, 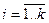 . Для интервального ряда используется полигон, который представляет собой ломаную соединяющую точки:
. Для интервального ряда используется полигон, который представляет собой ломаную соединяющую точки:
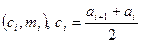 ,
, 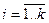 .
.
Гистограмма служит для представления, только интервальных вариационных рядов и имеет вид ступенчатых фигур с прямоугольным основанием, который имеет длину интервала 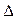 , а высота
, а высота 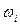 или
или 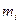 .
.
Кумулянта представляет собой ломаную соединяющую точки с координатами 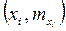 , где
, где 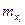 - накопленные частоты или для интервалов вариационного ряда: точки
- накопленные частоты или для интервалов вариационного ряда: точки 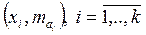 .
.
Определение: Эмпирические функции распределения 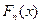 называются функциями вида:
называются функциями вида: 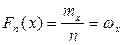 ,
, 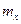 - накопленные частоты.
- накопленные частоты.
Определение: Основной характеристикой вариационного ряда называется его среднее арифметическое или выборочное среднее: 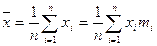 .
.
Для интервального ряда в качестве 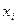 мы берём середину соответствия интервала.
мы берём середину соответствия интервала.
Вариационный размах: 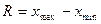 .
.
Выборочная дисперсия: 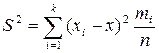 ,
, 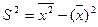 ,
, 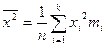 .
.
Выборочное среднее квадратичное отклонение: 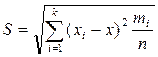 .
.
 2014-02-02
2014-02-02 4391
4391