Основные понятия дисперсионного анализа. Однофакторный дисперсионный анализ

В практике деятельности часто возникает необходимость выявления и оценки влияния отдельных факторов на изменчивость какого-либо признака значения, которого могут быть получены опытным путём виде реализации некоторой случайной величины 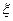. Под факторами будет пониматься независимые различные показатели. Дисперсионный анализ позволяет установить степень влияния факторов на изменчивость признаков. Количество факторов может быть различно. По количеству факторов различают однофакторный и двухфакторный анализ. Идея дисперсионного анализа заключается в том, что дисперсия изучаемого признака раскладывается на сумму составляющих её дисперсий.

Например: 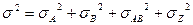, где

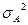- дисперсия, вызванная влиянием фактора ,

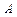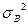- дисперсия, вызванная влиянием фактора ,

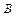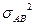- дисперсия, вызванная влиянием фактора ,

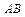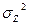- дисперсия, вызванная некоторым неучтённым фактором ,

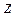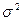- дисперсия изучаемого признака.

Мы будем рассматривать однофакторный дисперсионный анализ.

Однофакторный дисперсионный анализ

Будем считать, что некоторый фактор 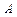изучается следующим образом:

На каждом из 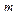уровней проводится по 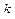измерений 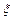. Данные эксперимента представлены в виде следующих таблиц:

№ набл.	Уровни факторов
A1	A2	…	Aj	…	Am
	x11	x12	…	x1j	…	x1m
	x12	x22	…	x2j	…	x2m
…	…	…	…	…	…	…
k	xk2	xk2	…	xkj	…	xkm
			…		…

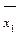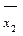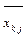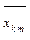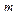уровней по 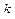измерений .

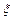Факторы .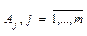

Будем рассматривать гипотезу:

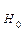: фактор 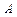не влияет на .

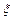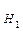: фактор 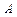влияет на .

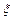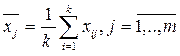- групповые средние.

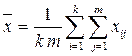- общая выборочная средняя принимаемая .

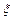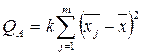- фактическая сумма квадратов отклонений групповых средних от общих средних.

Эта величина характеризует рассеивание между группами:

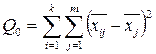- остаточная сумма квадратов отклонений, значения уровня фактов, от групповой средней.

Эта величина характеризует рассеивание внутри группы:

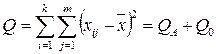- общая сумма квадратов отклонений выборочных значений от общего среднего.

На основании выше перечисленных формул рассчитаем следующие величины:

.

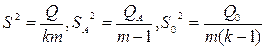Для выяснения влияния фактора 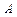на признак 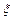сравниваются 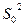и 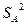. Влияние фактора 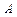на признак 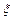считается заданным при заданном уровне 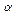, если выполняется услови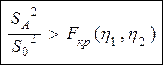е: , где 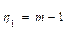, 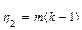. Если данное неравенство не выполняется, то влияние считается незначительным.

Пример:

В таблице приведены данные по объёмам работы выполненной на стройке за смену для 4 бригад. Проверить влияет ли состав бригады на объём выполненной работы.

№	№ бригады:
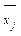	142,75	150,25	147,5	152,75

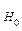: не влияет;

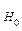: влияет.

Решение:

, , .

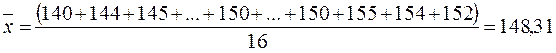
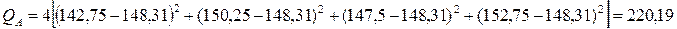
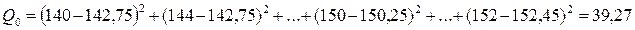
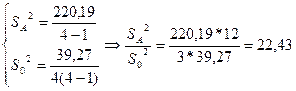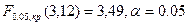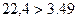Оценим степень этой зависимости с помощью коэффициента детерминирования:

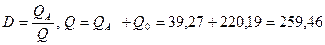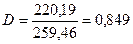, , 84,9 % общего изменения ежедневного объёма выработки связанного с работой смены.