2014-02-02
1421
Представим некоторую непрерывную функцию x (t) с интегрируемым квадратом в пространстве L2 (T) через произвольную ортогональную систему базисных функций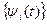 
векторов 
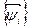, образующий ортогональный базис в L2 (T). Ортогональность функций означает, что
(*)
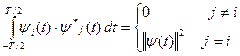В соответствие с 1.2.4. (5*) получаем представление:
(**)
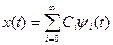где Сi – коэффициенты (координаты) разложения в ортогональный базис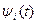 
. Полученное представление называют обобщенным рядом Фурье.
Рассматривая сигналы x (t) и 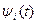как вектора 
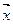и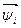 
пространства L2 (T), найдем скалярное произведение 
:
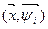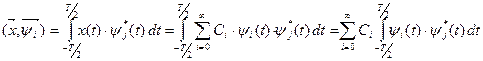
С учетом выражения (*) полученное равенство принимает вид:
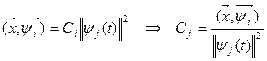(3*)
Представление (**) предполагает бесконечную размерность ортогонального базиса. На практике обычно используется усеченный ряд (**), в котором i меняется от 0 до n. Можно показать, что в том случае, когда коэффициент усеченного ряда Ci выбирается в соответствие с соотношением (3*), представление функции x (t) усеченным рядом обеспечивает минимальную среднеквадратическую ошибку аппроксимации.
Определим энергию сигнала x (t):
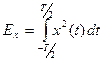
С учетом (**):
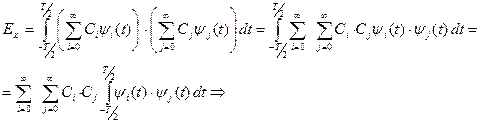
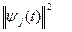
С учетом выражения (*) при условии, что x (t) и набор базисных функций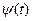 
являются действительными функциями, следует:
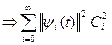
Т.о.,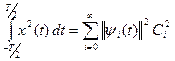 
(4*)
Если набор функций 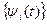является ортогональным (норма равна 1), то равенство (4*) имеет вид:
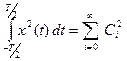(5*)
Равенство (4*) и (5*) называется равенством Парсеваля.
