Можно показать, что гармонический базис, основанный на использовании тригонометрический функций 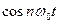 и
и 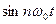 (n = 0, 1, 2, 3, …) является ортогональным на интервале
(n = 0, 1, 2, 3, …) является ортогональным на интервале 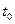 ¸
¸ 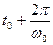 . В соответствие с выражением для обобщенного ряда Фурье, интегрируемая в квадрате функция f (t) может быть представлена на этом интервале в виде ряда:
. В соответствие с выражением для обобщенного ряда Фурье, интегрируемая в квадрате функция f (t) может быть представлена на этом интервале в виде ряда:
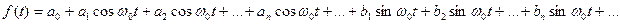
Введем обозначение 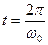 , тогда:
, тогда:
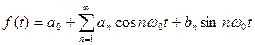 (*)
(*)
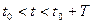
Выражение (*) представляет собой тригонометрическую форму ряда Фурье.
Коэффициенты an и bn вычислим по формулам обобщенного ряда Фурье:
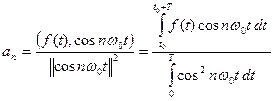 (**а)
(**а)
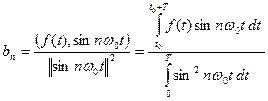 (**b)
(**b)
Если в формуле (**а) положить n = 0, то 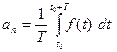 .
.
Поскольку при 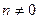 интеграл
интеграл 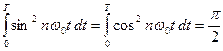 , следовательно,
, следовательно, 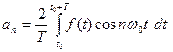 ,
, 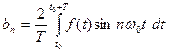 .
.
Из формулы для а0 следует, что первый член ряда а0 есть среднее значение или постоянная составляющая (нулевая гармоника) функций f(t) на том интервале. Полагая в формуле (*) 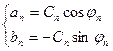 , её можно записать в виде:
, её можно записать в виде:
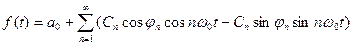
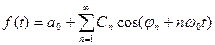 (***)
(***)
Где 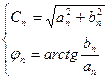 (из системы)
(из системы)
Представление ряда Фурье в (***), называемой амплитудно-фазовой, позволяет выделить спектр амплитуд (совокупность а0 и Сn) и спектр фаз (совокупность углов 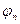 ).
).
 2014-02-02
2014-02-02 432
432








