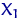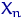Пример 3. Пусть , , — выборка объема из нормального распределения

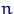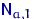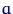Пусть , , — выборка объема из нормального распределения с неотрицательным средним . Ищем оценку для по первому моменту:

Однако по условию , тогда как может быть и отрицательно. Если 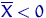, то в качестве оценки для 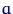более подойдет 0. Если же , в качестве оценки нужно брать . Итого: — «исправленная» оценка метода моментов.

2.5. Методы нахождения оценок: метод максимального правдоподобия

Метод максимального правдоподобия — еще один разумный способ построения оценки неизвестного параметра. Состоит он в том, что в качестве «наиболее правдоподобного» значения параметра берут значение , максимизирующее вероятность получить при 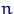опытах данную выборку 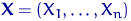. Это значение параметра зависит от выборки и является искомой оценкой.

Решим сначала, что такое «вероятность получить данную выборку», т.е. что именно нужно максимизировать. Вспомним, что для абсолютно непрерывных распределений их плотность 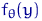— «почти» (с точностью до 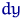) вероятность попадания в точку 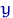. А для дискретных распределений вероятность попасть в точку 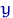равна 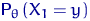. И то, и другое мы будем называть плотностью распределения . Итак,