2014-02-02
371
Теорема 2.
Состоятельность оценок метода моментов
Пусть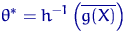 
— оценка параметра 
, полученная по методу моментов, причем функция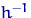 
непрерывна. Тогда 
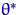состоятельна.
Может случиться так, что 
, тогда как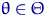 
. В этом случае оценку корректируют. Например, в качестве ОММ берут ближайшую к 
точку из 
или из замыкания .
