2014-02-02
347
Определение 3.
Статистика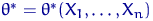 
называется несмещенной оценкой параметра 
, если для любого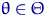 
выполнено равенство
.
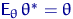Статистика 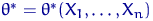называется состоятельной оценкой параметра , если для любого 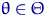имеет место сходимость
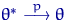при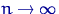 
.
Несмещенность — свойство оценок при фиксированном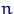 
. Означает это свойство отсутствие ошибки «в среднем», т.е. при систематическом использовании данной оценки.
Свойство состоятельности означает, что последовательность оценок приближается к неизвестному параметру при увеличении количества данных. Понятно, что при отсутствии этого свойства оценка совершенно «несостоятельна» как оценка.
2.3. Методы нахождения оценок: метод моментов
Метод моментов заключается в следующем: любой момент случайной величины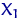 
(например, 
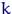-й) зависит, часто функционально, от параметра . Но тогда и параметр может оказаться функцией от теоретического 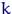-го момента. Подставив в эту функцию вместо неизвестного теоретического 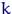-го момента его выборочный аналог, получим вместо параметра оценку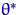 
. Пусть , 
, 
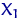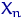— выборка объема 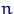из параметрического семейства распределений 
, где 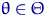. Выберем некоторую функцию 
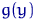так, чтобы существовал момент
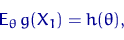
| (1) |
и функция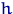 
была обратима в области 
. Тогда в качестве оценки 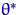для возьмем решение уравнения
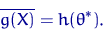
Или (что то же самое), сначала решаем уравнение (1) относительно , а затем вместо истинного момента берем выборочный:
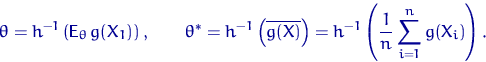
Чаще всего в качестве функции 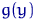берут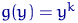 
. В этом случае
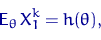
и, если функция 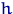обратима в области , то
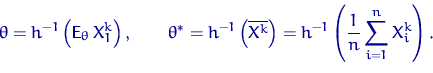
Можно сказать, что мы берем в качестве оценки такое (случайное) значение параметра , при котором истинный момент совпадает с выборочным.
