Аксиоматическое построение теории вероятностей. Замечание. С дальнейшим развитием естествознания возникла необходимость в формально-логическом обосновании теории вероятностей и её аксиоматическом

Замечание. С дальнейшим развитием естествознания возникла необходимость в формально-логическом обосновании теории вероятностей и её аксиоматическом построении. Исторически первым был подход С.Н. Бернштейна, основанный на качественном сравнении случайных событий по их большей или меньшей вероятности. Более современный подход А.Н Колмогорова связывает теорию вероятностей с современной математической теорией функций и теорией множеств.

Отправным пунктом аксиоматики Колмогорова является множество 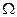, элементы которого называются элементарными событиями. Вместе с множеством 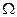рассматривается множество 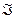подмножеств элементарных событий.

Определение 1. Множество 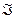называется алгеброй множеств, если выполнены следующие требования:

1) 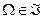, пустое множество ;

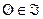2) ;

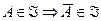3) .

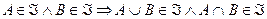Определение 2. Если в дополнение к требованиям 1) – 3) выполняется требование 4) 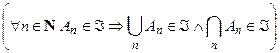, то множество 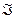называется -алгеброй.

Определение 3. Элементы 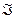называются случайными событиями.

Под операциями над случайными событиями понимаются операции над соответствующими множествами.