1. 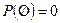 .
.
Доказательство. Свойство непосредственно следует из равенства 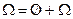 и аксиомы 3.
и аксиомы 3.
2. Для любого события А 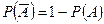 .
.
Доказательство. Так как 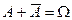 , то по аксиомам 2 и 3
, то по аксиомам 2 и 3 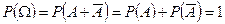 . Следовательно,
. Следовательно, 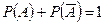 и
и 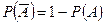 .
.
3. Для любого случайного события А 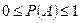 .
.
Доказательство. Свойство непосредственно следует из 1 и 2 и свойства 1.
4. Если событие А влечёт за собой событие В, то 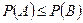 .
.
Доказательство. Событие В может быть представлено в виде 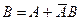 . Отсюда в силу аксиом 3 и 1 получаем
. Отсюда в силу аксиом 3 и 1 получаем 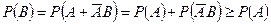 .
.
5. Для произвольных событий А и В 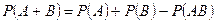 .
.
Доказательство. Поскольку в суммах 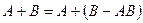 и
и 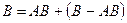 слагаемые являются несовместными событиями, то в соответствии с аксиомой 3
слагаемые являются несовместными событиями, то в соответствии с аксиомой 3
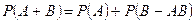 и
и 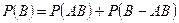 , тогда
, тогда
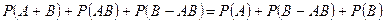 , откуда следует
, откуда следует
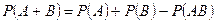 .
.
Замечание. Свойство 5 называют теоремой сложения для произвольных событий А и В.
Пример 1. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: 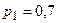 ;
; 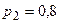 . Оба орудия выстрелили по цели. Найти вероятность попадания хотя бы одним из орудий.
. Оба орудия выстрелили по цели. Найти вероятность попадания хотя бы одним из орудий.
Решение. Пусть событие А – попадание в цель первого орудия, событие В – попадание в цель второго орудия. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А и В независимы. Вероятность события АВ (оба орудия попали в цель) 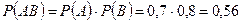 . Так как события А и В совместны, то искомая вероятность
. Так как события А и В совместны, то искомая вероятность 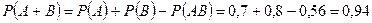 .
.
Следствие 1. Для произвольных событий А и В 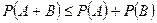 .
.
Доказательство следует из 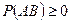 .
.
Следствие 2. Если 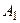 ,
, 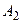 , …,
, …, 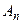 - произвольные события, то
- произвольные события, то 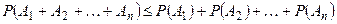 .
.
Доказательство проводится по индукции.
Замечание. Система аксиом Колмогорова непротиворечива так как существуют реальные объекты, которые всем этим аксиомам удовлетворяют.
Пример. Пусть 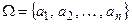 ,
, 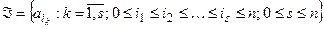 ,
, 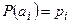 ,
, 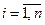 ,
, 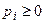 ,
, 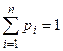 . Положив
. Положив 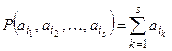 , удовлетворим аксиомам Колмогорова.
, удовлетворим аксиомам Колмогорова.
Система аксиом Колмогорова неполна: даже для одного и того множества 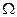 вероятности в множестве
вероятности в множестве 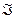 можно выбрать разными способами.
можно выбрать разными способами.
Пример. Игральная кость. 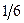 или
или 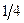 и
и 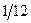 . Симметричная и несимметричная кости.
. Симметричная и несимметричная кости.
Неполнота системы аксиом теории вероятностей не является свидетельством их неудачного выбора или недостаточной работы по их созданию, а вызвана существом дела: в различных задачах могут встретиться явления, при изучении которых требуется рассматривать одинаковые множества случайных событий, но с различными вероятностями.
Дальнейшее развитие теории нуждается в дополнительном предположении, которое называется расширенной аксиомой сложения. Необходимость новой аксиомы объясняется тем, что в теории вероятностей постоянно приходится рассматривать события, подразделяющиеся на бесконечное число частных случаев.
Аксиома 4 (расширенная аксиома сложения). Если событие А равносильно наступлению хотя бы одного из попарно несовместимых событий 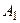 ,
, 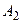 , …,
, …, 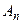 , …, то
, …, то 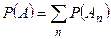 .
.
Замечание. Расширенная аксиома сложения может быть заменена равносильной ей аксиомой непрерывности.
Аксиома 4’ (аксиома непрерывности). Если последовательность событий 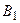 ,
, 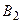 , …,
, …, 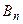 , … такова, что каждое последующее влечёт за собой предыдущее и произведение всех событий
, … такова, что каждое последующее влечёт за собой предыдущее и произведение всех событий 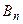 есть невозможное событие, то
есть невозможное событие, то 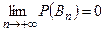 .
.
Теорема 1. Расширенная аксиома сложения и аксиома непрерывности эквивалентны.
Доказательство. 1. 4 – 4’. Пусть события 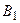 ,
, 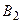 , …,
, …, 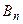 , … таковы, что
, … таковы, что 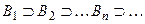 и для любого
и для любого 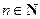 выполняется равенство
выполняется равенство 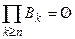 (*).
(*).
Очевидно, что
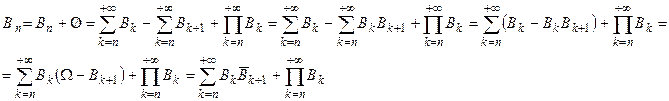
Так как события, стоящие в этой сумме попарно несовместны, то согласно расширенной аксиоме сложения 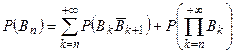 . Но в силу условия (*)
. Но в силу условия (*) 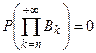 . Поэтому
. Поэтому 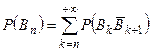 . То есть
. То есть 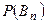 есть остаток сходящегося ряда
есть остаток сходящегося ряда 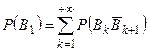 . Поэтому
. Поэтому 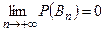 .
.
2. 4’ – 4. Пусть события 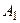 ,
, 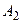 , …,
, …, 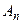 , …, попарно несовместны и
, …, попарно несовместны и 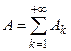 . Положим
. Положим 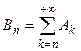 . По построению для любого
. По построению для любого 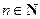
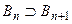 . Если событие
. Если событие 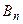 наступило, то наступило какое-нибудь из событий
наступило, то наступило какое-нибудь из событий 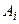 (
(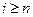 ) и, значит, в силу попарной несовместности событий
) и, значит, в силу попарной несовместности событий 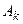 , события
, события 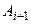 ,
, 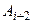 , … уже не наступили. Таким образом, события
, … уже не наступили. Таким образом, события 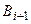 ,
, 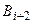 , … невозможны, следовательно, невозможно событие
, … невозможны, следовательно, невозможно событие 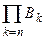 . По аксиоме непрерывности
. По аксиоме непрерывности 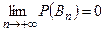 . Так как
. Так как 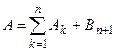 , то по обычной аксиоме сложения
, то по обычной аксиоме сложения 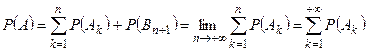 .
.
Замечание. Аксиоматика Колмогорова позволяет строить теорию вероятностей как часть теории меры, а вероятность рассматривать как неотрицательную нормированную аддитивную функцию множества.
Определение 4. Вероятностным пространством принято называть тройку символов 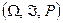 , где
, где 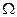 – множество элементарных событий,
– множество элементарных событий, 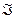 –
–  -алгебра подмножеств
-алгебра подмножеств 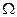 , называемых случайными событиями,
, называемых случайными событиями, 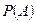 – вероятность, определённая на
– вероятность, определённая на  -алгебре
-алгебре 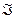 .
.
 2014-02-02
2014-02-02 5864
5864
