Прогнозирование неустойчивости методами теории катастроф

Теория катастроф представляет собой исследовательскую про­грамму изучения и прогнозирования неустойчивости различных систем*. Такое название она получила потому, что потеря устойчи­вости по своим проявлениям может быть катастрофична, даже если не приводит к гибели или разрушению системы, а лишь обуславли­вает переход к иной траектории развития.

Простейшая программа прогнозирования элементарной катаст­рофы в экономической или производственной системе может быть построена на основе данных о связи переменных, характеризую­щих ее поведение. Функции, описывающие эти связи, могут быть получены эконометрическими методами.

Например, связь двух переменных величин можно представить уравнением

у = х³/ 3 + а · х, (2)

где у и х — переменные, а — параметр; множитель 1/3 в первое слагаемое введен для упрощения преобразований.

Уравнение (2) представляет собой функцию, характер кото­рой определяется величиной параметра а. Если этот параметр поло­жителен, то функция носит монотонный характер, ее график — плавная монотонно возрастающая кривая. Но если параметр а умень­шается, то при нулевом его значении тип функции меняется. При нулевом значении параметра изменяются характер связи в системе и поведение системы, это изменение называют бифуркацией.

При отрицательной величине параметра а функция, описывае­мая уравнением (2), представляет собой уже немонотонную фун­кцию. Она имеет максимум и минимум при значениях х = ± а^1/2.

Катастрофа. Связь между переменными в определенной окрест­ности начала координат будет не однозначной. Одному значению переменной у будут соответствовать теперь три разных по величине значения переменной х. Таким образом, при монотонном плавном изменении переменной у переменная х будет изменяться скачкооб­разно. Это и будет катастрофа.

Если установлено, что между переменными, характеризующи­ми поведение системы, связь описывается уравнением вида (2), то можно утверждать, что в системе возможно проявление неус­тойчивости.

Если параметр а положителен, но выявлена тенденция его умень­шения, то можно считать, что система приближается к катастрофе. В обоих случаях необходимо продолжить изучение системы и выя­вить условия или возможные сроки наступления катастрофы, оце­нить ее вероятные последствия.

Тип элементарной катастрофы, определяемой связью, которая описывается уравнением (2), носит название катастрофы склад­ки, поскольку в пространстве трех координат — двух переменных и параметра а — поверхность, описываемая уравнением, имеет вид складки, начинающейся при а = 0 и углубляющейся по мере даль­нейшего уменьшения параметра. На рис. 3 показаны поверхности катастрофы складки и возможные траектории развития систем в условиях катастрофы этого типа.

Рис. 3 - Геометрия катастрофы складки и возможные траектории развития системы

Элементарная теория катастроф основывается на теореме Тома и классификации Арнольда. Они определили простейшие формы устойчивых и неустойчивых связей в системах — формы катастроф:

Каспоидные катастрофы:

складка

F = 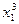+ a₁ – x₁+ M; (3)

сборка

F = ±(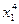 + а₂ · 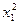+ а₁ · х₁) + М; (4)

ласточкин хвост

F=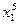 + а₃- 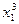+ а₂ - 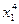+ а₁· х₁ + М; (5)

бабочка

F= ±(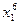 + а₄ · 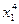+ а₃ · 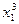+ а₂ ·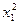+ а₁· х) + М; (6)

вигвам

F= 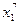+ а₅ · 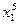+ а₄ · 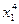+ а₃ · 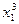+ а₂ ·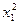+ а₁· х + М. (7)

Омбилические катастрофы:

эллиптическая омбилика

F= 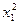х₂ — + а₃ · 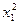+ а₂ · х₂ + а₁ · х₁ + N; (8)

гиперболическая омбилика

F= 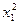х₂ + + а₃ · 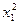+ а₂ · х₂ + а₁ · х₁ + N; (9)

параболическая омбилика

F= ±(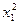х₂ +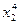 + а₄ · 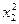+ а₃ · 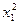+ а₂ · х₂ + а₁ · х₁) + N; (10)

вторая эллиптическая омбилика

F = 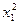х₂ - + а₅ ·+ а₄ ·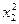+ а₃ · 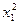+ а₂ · х₂ + а₁ · х₁) + N (11)

вторая гиперболическая омбилика

F = 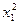х₂ + + а₅ ·+ а₄ ·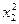+ а₃ · 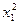+ а₂ · х₂ + а₁ · х₁) + N (12)

символическая омбилика

F = ±(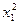++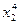 а₅ · x₁ · 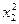+ а₄ ·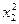+ а₅ · x₁ ·x₂ + а₂ · х₂ + а₁ · х₁) + N (13)

Здесь М— функция вида 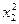+...+ 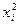— —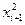... — 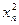, (1 ≤ i ≤ п);

N — функция вида 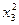+...+ 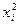— —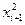... — 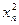, (2 ≤ i ≤ п);

x_i — взаимосвязанные переменные, характеризующие систему;

a₁... a_s — параметры, величина которых определяет условия катастрофы; п — общее число переменных;

F — функция, которая может быть при­равнена к еще одной переменной в первой степени или любой по­стоянной величине, например нулю. Все члены уравнения указаны с точностью до постоянных множителей и слагаемых.

Каспоидные катастрофы связаны с неустойчивостью связи од­ной переменной х₁ со всеми другими, а омбилические катастрофы — с неустойчивостью связи двух переменных х₁ и х₂ со всеми другими.

Программа анализа возможностей появления элементарных ка­тастроф связана с оценкой возможности описания связей в систе­мах уравнениями типа уравнений элементарных катастроф (3)— (13).

На практике программа может быть реализована, если можно получить регрессионные уравнения связей в системах. Уравнения устойчивых связей имеют вид

F=x₁ + x₁² + M; (14)

F= х₁ + х₂ + х₁ · х₂ + 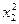+ + 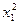N. (15)

Здесь по-прежнему все члены уравнения указаны с точностью до постоянных множителей.

Если по уровню детерминации, уровню значимости регресси­онное уравнение одной из катастроф превосходит регрессионное уравнение связи устойчивого характера, то следует считать ката­строфу возможной и дать для нее прогноз.

Флаги катастроф представляют собой косвенные признаки, по которым можно судить о возможности или наличии катастрофы в системе. К сожалению, для экономических и производственных систем при эмпирическом рассмотрении можно с уверенностью указать лишь один признак, флаг. Этот флаг — аномальная диспер­сия.

Признаком возможного приближения катастрофы является на­растание дисперсии или размахов колебаний величин, характеризую­щих систему. Этот флаг, как известно, успешно используется при статистическом регулировании качества продукции в серийном и массовом производстве.

Возможно, в отдельных случаях могут быть полезны и другие флаги. Их обнаружение будет свидетельствовать о наличии или воз­можности катастрофы и необходимости изучения устойчивости системы. Флаги могут быть объединены в две группы:

1) возможность существования более чем одной траектории устойчивого развития или равновесия; скачкообразное, быстрое изменение характеристик; большие изменения характеристик при малых управленческих воздействиях; проявления гистерезиса, то есть сравнительные трудности возврата системы к характеристикам предыдущего состояния;

2) различия в реакциях на одни и те же воздействия при неизменных условиях; замедление затухания колебаний характеристик; увеличение частоты колебаний.

Пример. Оценим устойчивость экономического развития СССР на основе данных о годовых темпах прироста национального дохо­да как о функции темпов прироста производства предметов по­требления и темпов прироста капиталовложений за период с 1951 по 1986г..

Для всего долгосрочного периода продолжительностью 36 лет может быть получена регрессионная модель устойчивого развития

у = 0,67 x₁ + 0,27 х₂, d = 63,3%, z ≤ 0,01%, (16)

где у — годовой прирост национального дохода, в %; л, и х₂ — годовые приросты соответственно производства предметов потреб­ления и капиталовложений, в %, d — уровень детерминации моде­ли, z — уровень значимости гипотезы об отсутствии связи в форме регрессионной модели.

Модели неустойчивого развития имеют вид моделей катастроф складки

у = -0,00125 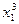+ 1,1 x₁, d = 61,3%, z < 0,01%; (17)

у = -0,00125 + 1,0 x₂, d = 40,4%, z < 0,01%. (18)

Поскольку модели элементарных катастроф лишь незначитель­но детерминированы по сравнению с моделью устойчивого разви­тия, то сделать уверенное заключение об устойчивости развития за период 1951—1986 гг. нельзя. Для периодов до второй половины 60-х годов наиболее детерминированными оказываются модели устойчивого развития. Например, для 1951 — 1960 гг. наиболее детермини­рованной оказывается модель

у = 0,52 х₁ + 0,36 х², d = 32,3%, z = 3,2%; (19)

Для периодов со второй половины 60-х до конца 80-х годов, наи­более детерминированными оказываются модели катастроф. Для 1966—1972 гг. наиболее детерминированной оказалась модель ката­строфы вида

у = -0,012 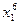+ 2405 х₁ - 1043 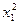+ 160,2 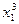- 9,20 ,

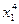d=93%, z = 4%; (20)

Для периода 1973—1980 гг. наиболее детерминированной оказа­лась модель катастрофы складки

у= -0,0185 + 1,71 x₂, d = 69%, z = 0,03%. (21)

Таким образом, в 50-х и первой половине 60-х годов развитие можно считать сравнительно устойчивым. Со второй половины 60-х и в 70—80-х годах тенденции неустойчивости стали нарастать, при­няли характер сложных катастроф. Полученные результаты свиде­тельствуют о том, что глубоким кризисным явлениям в экономике предшествовала потеря устойчивости экономического развития со второй половины 60-х годов.

Пример. Оценить устойчивость развития российской экономики в период кризиса. Адекватные модели устойчивых связей прироста ВВП с приростами производства в сельском хозяйства и в про­мышленности вообще получить невозможно. Это неудивительно, так как кризис и есть катастрофа. Для периода 1990—1995 гг. функ­ция прироста ВВП может быть представлена регрессионной моде­лью катастрофы типа эллиптической омбилики

у = 0,00766 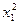х₂ – 0,0181 + 0,833 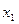+ 2,58 х₂ + 0,456 · х₂²,
d = 99,9%, z = 0,87%, (22)

где у — прирост ВВП, в %; x₁ и х₂ — приросты производства продукции соответственно сельского хозяйства и промышленности.

С использованием полученной модели рассчитаны возможные величины изменения ВВП в зависимости от возможных изменений объемов производства продукции отраслей. Данные представлены в табл. 2.

Таблица 2 - Возможное изменение ВВП России в 1990—1995 гг., обусловленное неустойчивостью развития

Изменение объемов сельскохозяйствен­ного производства,%	Изменение ВВП при изменении объемов промышленного произ­водства, %
	+ 5	+ 1		-1	-5
+5 +1 -1 -5	-21,4 -25,7 -26,0 -27,4 -29,0	+ 1,3 -2,2 -3,0 -3,9 -7,0	+4,2 +0,8 -0,8 -4,2	+6,2 +2,9 +3,1 + 1,3 -2,2	+6,9 +4,5 +3,7 +2,9 -1,4

Для прогнозирования поведения экономической системы в ус­ловиях катастрофы необходимо построить модели более коррект­ные, чем модели (17)—(22), которые пригодны лишь для оцен­ки принципиальной возможности катастрофы. В составе коррект­ных регрессионных уравнений моделей должны быть, как извест­но, постоянные члены.

Кроме того, следует иметь в виду, что уравнения элементарных катастроф (3)—(12) записаны в главных осях. Если используе­мые в анализе переменные независимы, между ними не обнаружи­ваются корреляционные связи, то для приведения к главным осям достаточно лишь перенести начало координат. Тогда, например, простейшее регрессионное уравнение катастрофы можно отыски­вать не в виде (3), а в виде х₂ = а₄ + а₂· (х₁ – а₃)³ + а₁ · (х₁ — а₂), или в виде х₂ = а₂ 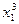- 3·x₁² · a₂ · a₃ + 3·x₁ · a₂ · a₃² + a₁ ·x₁ – a₁ ·x₂.

Получив корректное уравнение катастрофы, следует изучить тра­екторию предшествующего развития системы и оценить перспек­тивы ее изменения.