Метод Рунге-Кутта 2го порядка с усреднением по производной

Заменим приращение:

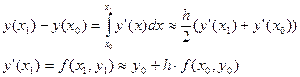
Окончательно получим следующую формулу:

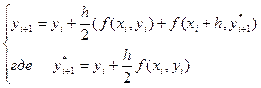
(6.4) Метод Рунге-Кутта 2го порядка с

усреднением по производной.

Локальная погрешность методов (6.3) и (6.4)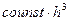

П.4. Сведение дифференциальных уравнений высших порядков к системе дифференциальных уравнений и её решение.

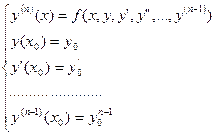Рассмотрим дифференциальное уравнение n ^ого порядка, разрешенное относительно старшей производной и Задачу Коши для данного уравнения:

- ДУ

Задача

Коши

(6.5) - начальные условия.

Чтобы свести З.К.(6.5) для ДУ n ^ого порядка к СДУ 1 ^ого порядка, поступаем следующим образом:

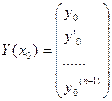
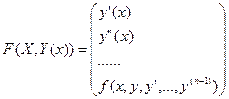введём вектор-функцию 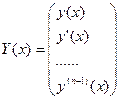, тогда З.К, (6.5)для ДУ n ^ого порядка сводится к СДУ 1 ^ого порядка:

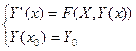(6.6)

где;

Итак, вместо З.К. (6.5) для ДУ n ^ого порядка мы получили З.К. (6.6) для СДУ 1 ^ого порядка, а её мы можем решить любым известным нам методом (Эйлера, Рунге-Кутта,…) с заменой в этих формулах скалярных величин y,f на векторные Y,F.

Пример сведения ДУ n^ого порядка к СДУ 1^ого порядка и нахождение решения по методу Эйлера:

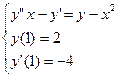
Имеем ДУ 2го порядка, сводим к СДУ 1го порядка для 2х уравнений:

Вводим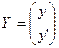

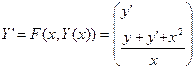
фиксируем шаг: h=0,1

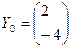
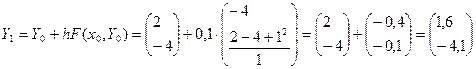
Аналогичным образом находим