Законы распределения дискретных случайных величин
Определение 9. Если вероятность наступления случайного события в каждом испытании равна 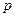 , то вероятность того, что случайное событие появится в этих
, то вероятность того, что случайное событие появится в этих 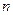 испытаниях ровно
испытаниях ровно 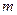 раз, выражается формулой Бернулли:
раз, выражается формулой Бернулли: 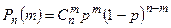 . Закон распределения дискретной случайной величины
. Закон распределения дискретной случайной величины  , которая может принимать
, которая может принимать 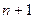 значение {0, 1, 2, …,
значение {0, 1, 2, …, 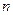 }, описываемый формулой Бернулли, называется биномиальным.
}, описываемый формулой Бернулли, называется биномиальным.
Замечание. Для биномиального закона распределения 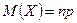 ,
, 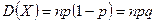 ,
, 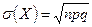 , мода
, мода 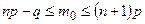 .
.
Доказательство. 1) Пусть случайная величина Х – число наступлений события А в 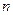 независимых испытаниях. Общее число Х появления события А в этих испытаниях складывается из чисел появления события А в отдельных испытаниях. Поэтому, если случайные величины:
независимых испытаниях. Общее число Х появления события А в этих испытаниях складывается из чисел появления события А в отдельных испытаниях. Поэтому, если случайные величины:  – число появлений события в первом испытании,
– число появлений события в первом испытании, 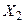 – во втором, и т.д.,
– во втором, и т.д., 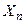 – в
– в 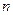 -ом, то общее число появлений события
-ом, то общее число появлений события 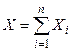 . Тогда по свойству 3 математического ожидания имеем
. Тогда по свойству 3 математического ожидания имеем 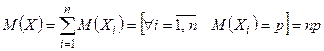 .
.
2) Так как величины  ,
, 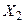 , …,
, …, 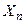 взаимно независимы (исход каждого испытания не зависит от исходов остальных испытаний), то по свойствам дисперсии
взаимно независимы (исход каждого испытания не зависит от исходов остальных испытаний), то по свойствам дисперсии
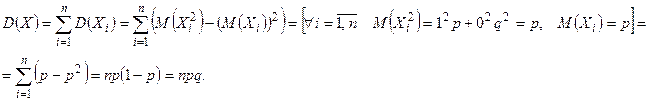
Отсюда следует, что 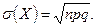 Мода (см. § 10):
Мода (см. § 10): 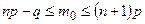 .
.
 2014-02-02
2014-02-02 656
656








