Замечание. Кроме свойств функции распределения, указанных в п. 12.2, функция распределения непрерывной случайной величины обладает своими специфичными свойствами.
Свойство 1. Вероятность того, что непрерывная случайная величина Х примет одно определённое значение, равна нулю.
Доказательство: Так как для любых 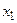 и
и 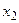 из неравенства
из неравенства 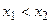 следует, что
следует, что 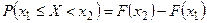 , то, полагая
, то, полагая 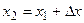 , имеем:
, имеем: 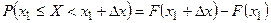 .
.
Переходя к пределу при  , в силу непрерывности
, в силу непрерывности  получаем, что
получаем, что 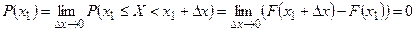 .
.
Следствие. Для непрерывных случайных величин справедливо для любых 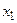 и
и 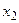
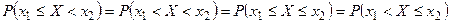 .
.
Замечание. Не представляет интереса говорить о вероятности того, что случайная величина примет одно возможное значение. Имеет смысл рассматривать вероятность попадания случайной величины в определённый промежуток, возможно, сколь угодно малый. Тем не менее, неправильно думать, что 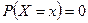 говорит о том, что событие
говорит о том, что событие 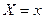 невозможно.
невозможно.
Свойство 2. Если возможные значения случайной величины принадлежат промежутку 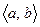 , то 1)
, то 1)  при
при 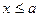 , 2)
, 2) 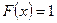 при
при  .
.
Доказательство. В первом случае событие невозможно, во втором – достоверно.
Свойство 3.  . В силу определений.
. В силу определений.
 2014-02-02
2014-02-02 791
791








