Определение 14. Модой дискретной случайной величины Х называется её наиболее вероятное значение.
Замечание. Геометрически мода является абсциссой той точки полигона распределения, ордината которой максимальна.
Определение 15. Начальным моментом порядка 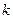 случайной величины Х называется математическое ожидание величины
случайной величины Х называется математическое ожидание величины 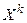 :
: 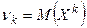 .
.
Замечание 1. В частности, 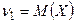 ,
, 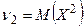 .
.
Замечание 2. Пользуясь определением моментов, дисперсию можно записать в виде 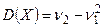 .
.
Замечание 3. Начальные моменты позволяют учесть большие, но маловероятные значения случайной величины.
Определение 16. Центральным моментом порядка 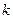 случайной величины Х называется математическое ожидание величины
случайной величины Х называется математическое ожидание величины 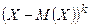 :
: 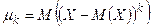 .
.
Замечание 1. В частности 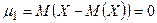
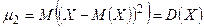 .
.
Замечание 2. Нетрудно показать, что 1) 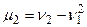 , 2)
, 2) 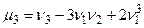 ,
,
3) 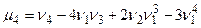 . Моменты более высоких порядков применяются редко.
. Моменты более высоких порядков применяются редко.
Замечание 3. Рассмотренные моменты называют теоретическими.
Пример 1. Случайная величина Х имеет ряд распределения:
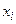
| ||||
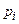
| 0,4 | 0,2 | 0,1 | 0,3 |
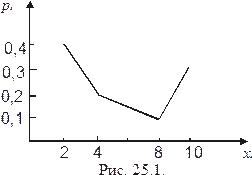 Построить многоугольник распределения, найти функцию распределения вероятности и построить ее, найти математическое ожидание, дисперсию, СКО и моду случайной величины Х.
Построить многоугольник распределения, найти функцию распределения вероятности и построить ее, найти математическое ожидание, дисперсию, СКО и моду случайной величины Х.
Решение. 1) В прямоугольной системе координат 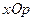 отметим точки
отметим точки 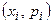 и соединим их последовательно ломаными отрезками. Получим многоугольник распределения (см. рис. 25.1).
и соединим их последовательно ломаными отрезками. Получим многоугольник распределения (см. рис. 25.1).
2) Найдём функцию распределения вероятности.
Если 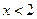 , то
, то 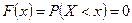 .
.
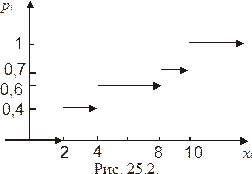 Если
Если 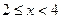 , то
, то 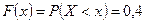 .
.
Если 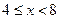 , то
, то 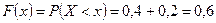 .
.
Если 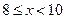 , то
, то 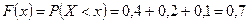 .
.
Если 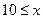 , то
, то 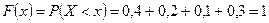 .
.
Построим график функции распределения вероятности (см. рис. 25.2).
3) Найдём числовые характеристики случайной величины Х.
а) математическое ожидание: 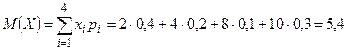 ;
;
б) дисперсия: 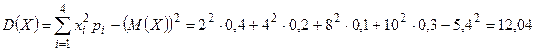 ;
;
в) СКО: 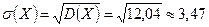 ;
;
г) мода случайной величины Х – это такое её значение, которому соответствует наибольшая вероятность; наибольшая вероятность 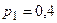 соответствует значению
соответствует значению 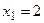 ; поэтому
; поэтому 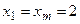 .
.
 2014-02-02
2014-02-02 541
541







