Функция распределения и плотность распределения непрерывной случайной величины. Непрерывные случайные величины их числовые характеристики и законы распределения

Непрерывные случайные величины их числовые характеристики и законы распределения

Пусть дана случайная величина .

Определение 1. Пусть для Х существует неотрицательная функция 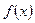, удовлетворяющая для любых 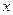равенству 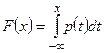. Тогда случайная величина Х называется непрерывной.

Замечание. Функция 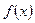является законом распределения вероятностей непрерывной случайной величины и называется функцией плотности распределения вероятностей или дифференциальной функцией распределения вероятностей.

Определение 2. График функции 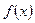называется кривой распределения.

Определение 3. Если 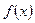– плотность распределения вероятности непрерывной случайной величины, то функция распределения вероятности 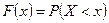имеет вид: 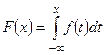. В этом случае функцию 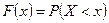называют интегральной функцией распределения вероятности.