Свойства п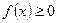лотности вероятности

Свойство 1. . (По определению)

Свойство 2. (если все значения случайной величины заключены в интервале , то ).

Доказательство. Событие: Х попадет в интервал – достоверно.

Свойство 3. Вероятность , что значение, принятое случайной величиной , попадет в промежуток , определяется формулой для любых 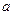и .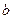

Доказательство. .

Замечание. Формула остаётся справедливой для отрезка и интервала.

Геометрический смысл плотности вероятности. Вероятность попадания непрерывной случайной величины в промежуток численно равна площади криволинейной трапеции, ограниченной осью ОХ и кривой распределения.

Следствие. Если 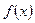непрерывна в точке 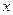, то с точностью до бесконечно малых высших порядков .

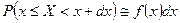Доказательство. .