Теорема Пуассона. Относительная частота события в 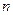 независимых испытаниях, в каждом из которых оно может произойти соответственно с вероятностями
независимых испытаниях, в каждом из которых оно может произойти соответственно с вероятностями 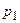 ,
, 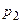 , …,
, …, 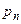 , при неограниченном увеличении
, при неограниченном увеличении 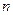 сходится по вероятности к средней арифметической вероятностей события в отдельных испытаниях:
сходится по вероятности к средней арифметической вероятностей события в отдельных испытаниях: 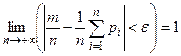 .
.
Доказательство непосредственно следует из теоремы Чебышева, если в качестве случайных величин 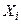 (
(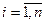 ) рассматривать случайные величины, имеющие каждая 2 значения 1 и 0 и распределение
) рассматривать случайные величины, имеющие каждая 2 значения 1 и 0 и распределение 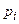 ,
, 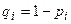 . Математические ожидания этих величин равны
. Математические ожидания этих величин равны 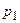 ,
, 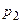 , …,
, …, 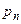 (
(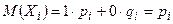 ), а дисперсии
), а дисперсии 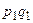 ,
, 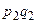 , …,
, …, 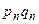 (
(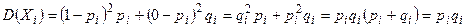 ) ограничены одним числом (
) ограничены одним числом (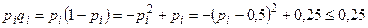 ).
).
 2014-02-02
2014-02-02 625
625








