Теорема Бернулли

Пусть вероятность наступления случайного события А в каждом из 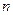независимых испытаний равна 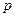. Требуется выяснить, какой примерно будет относительная частота появлений события.

Терема Бернулли. Если вероятность наступления случайного события А в каждом из 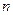независимых испытаний равна 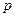, то вероятность того, что отклонение относительной частоты от вероятности 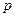по абсолютной величине будет сколь угодно малым, будет сколь угодно близка к единице, при условии, что число испытаний достаточно велико: для любого малого .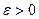

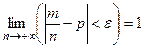Доказательство. Обозначим 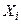(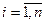) – дискретную случайную величину – число появлений события А в 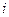-ом испытании. Для любого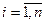 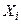может принять всего 2 значения: 1 (А наступило) с вероятностью 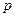и 0 (событие не наступило) с вероятностью 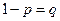. Случайные величины 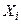(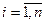) независимы, так как испытания независимы. Дисперсия любой случайной величины 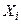(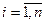) равна 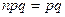(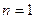– каждая величина характеризует ровно одно испытание, условия соответствуют закону Бернулли). Так как 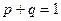, то 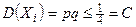(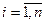), т.е. дисперсии равномерно ограничены. Тогда по следствию к теореме Чебышева имеем:

или (так как ) .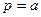

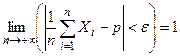Покажем, что – относительной частоте появления события А в 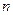независимых испытаниях. Действительно, каждая из величин 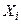(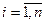) при появлении события в соответствующем испытании принимает значение, равное 1, следовательно, сумма 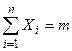числу появлений события А в 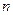независимых испытаниях. Следовательно, , тогда 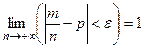. Теорема доказана.

Замечание 1. Из теоремы Бернулли не вытекает равенство . В теореме речь идёт о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании. Сходимость относительной частоты 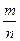к вероятности 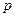есть сходимость по вероятности (в отличие от обычной сходимости, при отдельных значениях 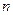неравенство 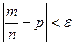может и не выполняться). Теорема Бернулли объясняет тот факт, что относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности.

Замечание 2. Непосредственным обобщением теоремы Бернулли является теорема Пуассона, когда вероятности событий в каждом испытании различны.