Теперь, когда мы определились, какую же величину будем искать, давайте воспользуемся довольно часто используемым в физике приёмом. Мы попытаемся “угадать” искомое распределение. А проверку того, что мы угадали правильно, мы получим, сравнивая результаты нашей теории с экспериментом.
Из чего мы должны исходить при нахождении искомого распределения? Оказывается, у нас есть 2 отправных момента:
1 Распределение молекул по скоростям должно быть симметричным относительно начала координат. Это следует из того, что в равновесном состоянии все направления в пространстве равноправны. Если бы это было не так, то был бы дрейф молекул – поток молекул в каком-либо одном направлении, связанный с переносом, например, энергии. В равновесном состоянии никаких потоков нет.
2 Исходя из того, что кинетическая энергия молекул, заключённых в любом сосуде, должна быть конечной, в искомом распределении не должно быть бесконечно большой скорости даже у одной молекулы.
Итак, предположим, что функция распределения молекул по проекциям скорости имеет вид
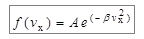 . (7.5)
. (7.5)
Действительно, такой вид функции распределения удовлетворяет двум нашим исходным требованиям:
1) эта функция – чётная относительно начала координат;
2) 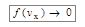 при
при 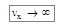 .
.
Теперь наша задача – определение коэффициентов А и b. Для определения коэффициента А воспользуемся условием нормировки (7.4):
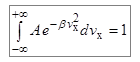 . (7.6)
. (7.6)
Сделаем замену переменных в интеграле:
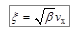 , и
, и 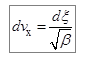 . (7.7)
. (7.7)
Тогда вместо выражения (7.6) получим
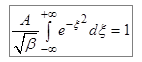 . (7.8)
. (7.8)
В выражении (7.8) мы получили табличный интеграл Пуассона:
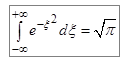 . (7.9)
. (7.9)
Подставим значение интеграла Пуассона в выражение (7.8):
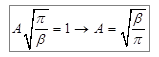 . (7.10)
. (7.10)
Таким образом,
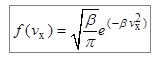 . (7.11)
. (7.11)
Аналогично можно получить, что
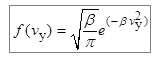 ,
, 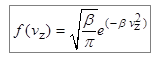 .
.
На основании теоремы о вероятности независимых событий[12] полная функция распределения имеет вид:
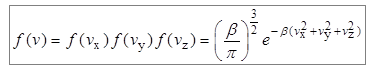 . (7.12)
. (7.12)
Для определения константы b с помощью функции распределения (7.12) вычислим среднее значение кинетической энергии, уже зная ответ. А именно 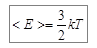 . На основании формулы (7.2) мы можем записать, что:
. На основании формулы (7.2) мы можем записать, что:
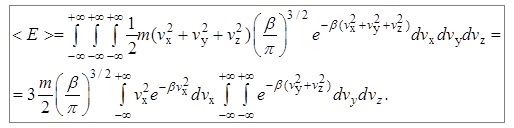 (7.13)
(7.13)
Выражение (7.13) представляет собой произведение трех одинаковых интегралов, поэтому в выражении (7.13) появляется множитель 3. Оставшееся выражение также равно произведению трех интегралов – по переменным v x, v y и v z:
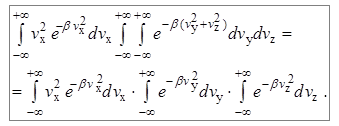 (7.14)
(7.14)
Вычислим интеграл по переменной v x. Снова сделаем замену переменных в выражении (7.7) и получим, что
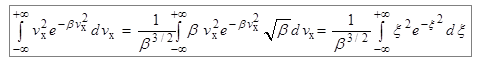 (7.15)
(7.15)
Последний интеграл в выражении (7.14) также является табличным (и тоже называется интегралом Пуассона):
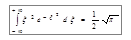 . (7.16)
. (7.16)
Таким образом,
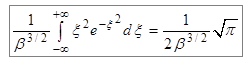 . (7.17)
. (7.17)
Второй и третий интегралы мы фактически уже вычисляли – они отличаются от интеграла в выражении (7.6) только другим обозначением переменной интегрирования. Следовательно, каждый из этих интегралов равен  . Теперь соберём весь наш тройной интеграл (7.14) и получим
. Теперь соберём весь наш тройной интеграл (7.14) и получим
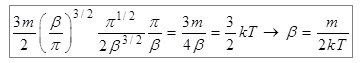 . (7.18)
. (7.18)
Окончательный вид функции распределения:
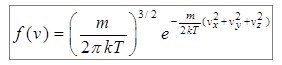 . (7.19)
. (7.19)
Выражение (7.19) называется функцией распределения Максвелла по направлениям скоростей. Она имеет вид, показанный на рисунке 7.1.

Рисунок 7.1 – Распределения Максвелла по направлениям скоростей
Напомним, что выражение 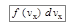 дает вероятность
дает вероятность 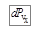 того, что проекция скорости молекулы на ось х лежит в пределах от
того, что проекция скорости молекулы на ось х лежит в пределах от  до
до 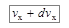 . А если мы умножим
. А если мы умножим 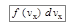 на число молекул в сосуде N, то получим
на число молекул в сосуде N, то получим 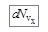 – число молекул, имеющих проекцию скорости на ось х в пределах от
– число молекул, имеющих проекцию скорости на ось х в пределах от  до
до 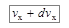 . Так как движения в положительном и отрицательном направлениях оси Ох равновероятны, то эта функция симметрична. Кроме того, в условиях термодинамического равновесия в обоих направлениях оси Ох движется в среднем одинаковое количество молекул, а это значит, что среднее значение проекции скорости
. Так как движения в положительном и отрицательном направлениях оси Ох равновероятны, то эта функция симметрична. Кроме того, в условиях термодинамического равновесия в обоих направлениях оси Ох движется в среднем одинаковое количество молекул, а это значит, что среднее значение проекции скорости  , вычисленное для всех молекул, будет равно 0. Поэтому функция
, вычисленное для всех молекул, будет равно 0. Поэтому функция 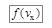 имеет максимум при
имеет максимум при  = 0. Аналогично, умножив функцию (7.18) на
= 0. Аналогично, умножив функцию (7.18) на 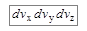 мы получаем вероятность того, что компоненты скорости молекулы лежат в пределах от
мы получаем вероятность того, что компоненты скорости молекулы лежат в пределах от 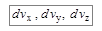 до
до 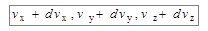 . Число молекул, скорости которых находятся в указанном интервале, будет равно
. Число молекул, скорости которых находятся в указанном интервале, будет равно
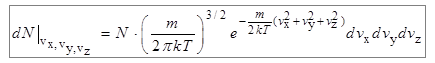 . (7.20)
. (7.20)
 2014-02-02
2014-02-02 1503
1503