В модели идеального газа одноатомную молекулу рассматривают как материальную точку, которая одновременно может двигаться вдоль трех координат. В этом случае говорят, что молекула обладает тремя степенями свободы. Вообще, степенями свободы называют минимальное число независимых координат, которыми можно задать положение тела в пространстве.
Рассмотрим пример абсолютно твёрдого несимметричного тела. Оно имеет шесть степеней свободы: три из них описывают поступательное движение центра масс тела и три вращательных степени свободы, которые описывают вращение вокруг трех взаимно перпендикулярных осей (рис. 6.3, а). Если мы соединим две материальные точки жёсткой связью, то при вращении вокруг оси, проходящей через точки, положение такой системы в пространстве не изменится (рис. 6.3, б), т.е. число степеней свободы будет равным пяти. Вообще, говорят, что любая жёсткая связь уменьшает число степеней свободы системы на единицу. Пусть теперь две материальные точки связаны не жёсткой связью, а упругой. В этом случае такая система имеет шесть степеней свободы: три поступательных, две вращательных и одну колебательную (рис. 6.3, в).
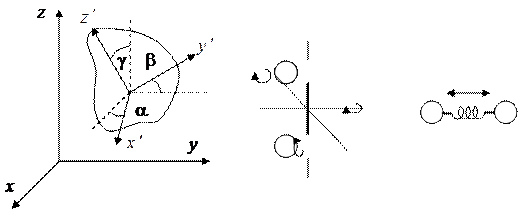
а б в
а – абсолютно твердое несимметричное тело; б – две материальные
точки, связанные жесткой связью; в – две материальные точки,
связанные упругой связью
Рисунок 6.3 – Степени свободы
В классической физике двухатомную молекулу рассматривают как две материальные точки, соединенные или жёсткой, или упругой связью. Тогда двухатомная молекула может обладать либо пятью степенями свободы (для жёсткой связи), либо шестью – при наличии упругой связи между молекулами. Но сколько бы степеней свободы не имело тело (молекула) – три из них всегда поступательные, и на них приходится энергия 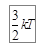 .
.
В статистической физике доказывается закон о равнораспределении энергии по степеням свободы. Согласно этому закону на каждую степень свободы приходится в среднем одинаковая кинетическая энергия, равная 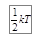 . Таким образом, средняя энергия теплового движения молекулы должна равняться:
. Таким образом, средняя энергия теплового движения молекулы должна равняться:
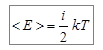 , (6.16)
, (6.16)
где полное число степеней свободы i определяется как
 . (6.17)
. (6.17)
Двойка в выражении (6.17) отражает тот факт, что колебательная степень свободы имеет удвоенную энергетическую ёмкость. В то время как поступательные и вращательные степени свободы несут только кинетическую энергию, на колебательную степень свободы приходится и кинетическая и потенциальная энергии. Причём, как мы знаем, в случае колебаний средние значения этих энергий равны между собой. Следовательно, средняя энергия, приходящаяся на колебательную степень свободы, будет равна 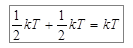 .
.
 2014-02-02
2014-02-02 4449
4449
