Опытные законы идеального газа

Идеальный газ – это идеализированная модель реальных газов, согласно которой:

1. Общий объем всех молекул газа пренебрежимо мал по сравнению с объемом сосуда, в котором находится газ.

2. Взаимодействие молекул между собой и стенками сосуда сводится к абсолютно упругим столкновениям.

Из первого предположения следует, что расстояния между молекулами намного превышают размеры молекул, и поэтому молекулы можно рассматривать как материальные точки. С другой стороны, при больших расстояниях между молекулами можно пренебречь силами притяжения и отталкивания между молекулами. Это обстоятельство оправдывает второе предположение. Напомним, что упругим называется удар, при котором механическая энергия соударяющихся тел остаётся постоянной. Оказывается, что очень многие реальные газы при нормальных условиях (комнатной температуре и атмосферном давлении) можно считать идеальными.

Термодинамическими параметрами, описывающими состояние данной массы газа, являются давление P, объём V и температура T [10]. Эти параметры состояния идеального газа связаны уравнением состояния идеального газа, которое называют уравнением Менделеева – Клапейрона:

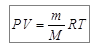. (6.2)

В уравнении (6.2) m – масса газа, M – его молярная масса. Таким образом, отношение m/M = v равно числу молей газа, R = 8,31 (Дж/моль?К) – универсальная газовая постоянная. Универсальная газовая постоянная равна произведению двух констант – числа Авогадро и постоянной Больцмана k = 1,38·10^-23 (Дж/К). Таким образом, выражение (6.2) можно переписать в виде

.

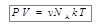Произведение vN _A = N равно числу молекул, которое содержится в массе газа m. С учётом этого:

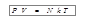. (6.3)

Теперь разделим обе части уравнения (6.3) на V. С учётом того, что N/V = n, где n – концентрация молекул, т.е. число молекул в единице объёма, вместо выражения (6.3) получим:

P = nkT. (6.4)

Уравнения (6.2), (6.3), (6.4) также называют уравнениями состояния идеального газа, записанными в разных формах.

Уравнение Менделеева – Клапейрона является обобщением опытных законов, описывающих поведение идеального газа в различных изопроцессах. Рассмотрим эти газовые законы. Перепишем уравнение (6.2) в виде:

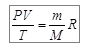. (6.5)

Из уравнения (6.5) следует, что при постоянной массе газа выполняется соотношение:

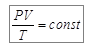, (6.6)

которое называют объединенным газовым законом.

1. Изотермический процесс: T = const, m = const.

Из уравнения (6.5) получаем закон Бойля-Мариотта:

,

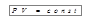для постоянной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная (рис. 6.1, а).

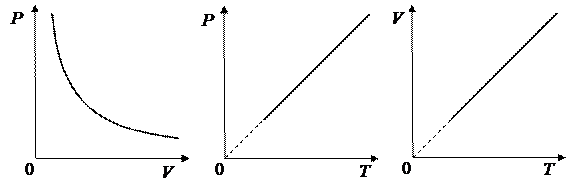
а б в

а – изотермический процесс; б – изохорный процесс; в – изобарный процесс

Рисунок 6.1 – Изопроцессы

2. Изохорный процесс: V = const, m = const.

При этих условиях выполняется закон Гей-Люссака:

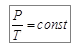, или ,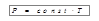

давление данной массы газа при постоянном объеме изменяется линейно с температурой (рис. 6.1, б).

3. Изобарный процесс: P = const, m = const.

В этом случае из выражения (6.6) получаем закон Шарля:

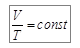, или ,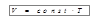

объем данной массы газа при постоянном давлении изменяется линейно с температурой (рис. 6.1, в).

Для смеси газов выполняется закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в неё газов:

,

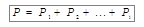где P _i– парциальное давление i -й компоненты смеси. Парциальное давление – это давление, которое производил бы один газ при том же объёме и температуре, если бы других газов не было. Парциальное давление можно найти из уравнения Менделеева – Клапейрона (6.2).