О знаках равенства и неравенства

Содержание

ГлаваI Введение

Глава II Классические неравенства в задачах

2.1О знаках равенства и неравенства

2.2Династия Бернулли

2.3Неравество Бернулли

2.4 Огюстен Коши – достижения в математике

2.5 Неравенство Коши

2.6 Христиан Гюйгенс

2.7 Неравенство Гюйгенса

2.8 В.Я. Буняковский

2.9 Неравенство Коши – Буняковского

Глава III Заключение

Литература

 

 

Введение

Неравенства разнообразны по природе участвующих в них объектов. Этими объектами могут быть числа, функции, интегралы, производные, которые порождают соответственно числовые, функциональные ит.п. неравенства. В свою очередь функциональные неравенства часто квалифицируют по разным признакам, например, алгебраические и транцендентные, линейные и нелинейные, с одной и со многими переменными, строгие и нестрогие, односторонние и двойные. Разнообразие методов и приемов решения неравенств обогащает и делает интересной эту тему.

Применение неравенств в математике многообраны:

· В алгебре, геометрии, математическом анализе при доказательстве теорем, отражающих функциональные свойства (возрастание, убывание, выпуклость, вогнутоть, сходимость, расходимость)

· В решение экстремальных задач (экстремальные свойства симметричных геометрических фигур, задачи на максимум и минимум, наибольшее и наименьшее значение, задачи математического программирования)

· В теории вероятностей и ее приложениях для изучения количественных характеристик случайных событий, величин, процессов (математическая статистика)

· В вычислительной математике для теоретического обоснования условий сходимости различных вычислительных алгоритмов и оценки погрешностей.

· В программировании.

Цель работы:

Исследование классических неравенств в алгебре и применение этих неравенств на других примерах.

Для достижения поставленной цели определены следующие задачи:

· Краткое изложение творческой деятельности ученых математиков: Якоба Бернулли, Коши, Гюйгенса и Буняковского.

· Исследование способов решения классических неравенств.

· Применение популярных неравенств в задачах.

Классические неравенства в задачах

О знаках равенства и неравенства.

При исследовании корней квадратного уравнения по дискриминанту и при построении графиков мы часто применяем наряду со знаком равенства и знаки неравенства.

В 1557г., когда Роберт Рекорд впервые ввел знак равенства, он мотивировал свое нововведение следующим образом: никакие два предмета не могут быть между собой более равными, чем два параллельных отрезка. Знак равенства Рекорда стал, однако, общеупотребительным лишь в 18 в., после того как им стали пользоваться Лейбниц и его последователи.

Исходя из знака равенства Рекорда, другой английский ученый Гарриот ввел употребляемые поныне знаки неравенства, обосновывая (в «Практике аналитического искусства», вышедшей в 1631 г. посмертно) нововведение (до него писали словами «больше», «меньше») следующим образом: если две величины не равны, то отрезки, фигурирующие в знаке равенства, уже не параллельны, а пересекаются. Пересечение может иметь место справа (>) или слева (<). В первом случае образованный знак неравенства будет обозначать - «больше», во втором - «меньше».

Несмотря на то что знаки неравенства были предложены через 74 года после предложенного Рекордом знака равенства. Они вошли в употребление намного раньше последнего. Одна из причин этого явления корениться в том, что типография применяла в то время для знаков неравенства уже имевшуюся у них латинскую букву V, тогда как наборного знака равенства (=) у них не было, а изготовлять его тогда было нелегко.

О понятии неравенства. Знаки неравенства (>,<) появились впервые в 1631 г., но понятие неравенства, как и понятие равенства, возникло в глубокой древности.

В развитии математической мысли без сравнения величин, без понятий «больше» и «меньше» нельзя было дойти до понятия равенства, тождества, уравнения. Приближенные вычисления (в том числе и, метод исчерпывания, современное понятие предела и др.) Связанны с понятием неравенства.

Некоторые неравенства древности.

В пятой книге «Начал» Евклида доказывается:

«Если - небольшое число в пропорции

где – положительные числа, то существует неравенство

»

В основном труде Папа Александрийского, названном «Математическое собрание» и написанном в 3 в., доказывается:

«Если , то »

Строгие и нестрогие неравенства В теории и в практических задачах встречаются знаки неравенства, соединенные со знаком равенства ≤(не больше) или ≥(не меньше).такие неравенства называются нестрогими в отличие от неравенств, содержащих знак или и называются строгими.

 

Символы ≥ и ≤ были введены в 1734 г. Французским математиком Пьером Буге. Позже их стали записывать так ≤, ≥ ﴾ 1 ﴿

Династия Бернулли

 

Род Бернулли дал девять крупных математиков, из них трех великих (Якоб, Иоганн, Даниил). Помимо математиков, среди Бернулли были историки, архитекторы, юристы, искусствоведы ит.д. Не менее тридцати представителей Бернулли обладали выдающимися талантами.

Кафедру математики Базельского университета (Швейцария г. Базель, 1460г. – основание университета) возглавляли 105 лет практически без перерыва. Профессорами того же университета (на разных кафедрах) Бернулли состояли более 200 лет. Кресло

академика парижской академии наук занято ими подряд 100 лет. Та же академия выдала десятки премий членам этой семьи. Пятеро математиков Бернулли были членами Петербургской академии наук, трое работали в Петербурге.

Необыкновенно устойчивая одаренность Бернулли, переходящая из поколения в поколение, проявляется у них в раннем развитии математического дарования, непреодолимом стремлении к точным наукам, широте и глубине знаний. Бернулли сделали значительный вклад в науку на заре становления и оформления «новой» математики (дифференциальное и интегральное исчисления, дифференциальные уравнения, ряды, теория вероятностей) ﴾2﴿

Якоб Бернулли

 

Якоб Бернулли родился 27 декабря 1654 г.. По желанию отца готовился к знанию протестантского священника. Окончил Базельский университет, где изучал философию, богословие и языки. Владел немецким, французским, английским, итальянским, латинским и греческими языками. Испытывая непреодолимое влечение к математике, изучал ее тайком от отца. В 1671 г. Получил степень магистра философии. С большим успехом читал проповеди на немецком и французском языках. В то же время продолжал пополнять свои знания по математике без учителя, почти без учебников.В Швейцарии того времени занятие математикой не обещало никаких выгод, так как соответствующих должностей было мало, и даже университетские преподаватели математики оплачивались крайне скудно. Несмотря на это, Якоб решил посвятит себя целиком математике. В 18 лет успешно занимался довольно трудной хронологической задачей об определении года юлианского календаря по данным солнечного периода и индиктиона.

20 августа 1676 г. Якоб отправился в длительное путешествие по Швейцарии, Франции, Италии, из которого возвратился в Базель лишь 20 мая 1680г. В Генуе Якоб прожил 20 месяцев. Здесь он был домашним учителем в семье Вальдкирхов. Дочь Елизавета потеряла зрение через несколько месяцев после рождения. Она обладала редкими способностями, свободно говорила на нескольких языках. Под руководством Якоба Елизавета изучала логику, историю, физику ит.д.

По возвращению в Базель Якоб публикует первую научную работу, посвященную теории комет. Здесь он высказался против общепринятого мнения, согласно которому комета – некий «воздушный феномен». Он утверждал, что кометы – небесные тела с определенными траекториями движения.

В 1682 г. Якоб отправляется в новое путешествие, на этот раз по Нидерландам и Англии. Он завязывает научные знакомства: с Х Гюйгенсом в Амстердаме, с королевским астрономом Фламстидом в Гринвиче и др. В октябре 1682 г. Возвращается в Базель и больше уже не выезжает никуда, если не считать лечения на курортах.

В 1682 г. Якоб получает приглашение на должность проповедника в Странсбурге, но отклоняет его, так как собирается посвятить себя целиком естественным наукам. В 1683 г. Начинает читать цикл лекций по экспериментальной физике в Базельском университете. В 1684 г. Поступает новое предложение, на этот раз из Гейдельберга, занять кафедру математики университета. Это предложение также отвергнуто: из-за предстоящей женитьбы Якоб не хотел оставлять родной город.

В октябре 1686 г. Оказывается вакантной должность профессора математики в Базельском университете.Успехи Якоба вматематике

Хорошо известны, и Сенат университета единодушно выдвинул на вакантную должность Якоба Бернулли. Вступление в должность состоялось15 февраля 1687г. Вряд ли присутствующие при этом

скромном акте представляли, что они являются свидетелями начала беспримерного в истории математики события: отныне кафедру будут занимать Бернулли на протяжении 100 лет. Члены же этой семьи будут профессорами родного университета в течение четверти тысячелетия, вплоть до второй половины XX в.

В 1692 г. Сравнительно молодой ученый серьезно заболел. Судя по описанию болезни, можно заключить, что Якоб сильно простудился.Организм не справился с заболеванием, развился туберкулез. К этому прибавились тяжелые переживания, вызванные ссорой с братом. Однако плодотворная научная деятельность не прекращалась и слава ученого все росла.В 1699г. Парижская академия наук впервые избрала 8 иностранных членов. В их числе наряду с Ньютоном, Лейбницем, О. Ремером были и братья Якоб и Иоганн Бернулли. В 1701г. Братья были избраны иностранными членами Берлинской академии наук (по представлению Лейбница).

Основные научные интересы Якоба были сосредоточены на развитии и приложениях анализа.

Спор между братьями возник в 1694-1695гг. в связи с недостаточно обоснованным подчеркиванием младшим братом своих заслуг за счет заслуг старшего.

Самомнение Иоганна и зависть внушила ему мысль о том, что Якоб ему уступает по уму, что его не следует считать значительным математиком. Видимые поводы для этого были: решения Иоганна блистало изяществом и простотой. Но он не мог не заметить, что за внешней громоздкостью работ брата кроется их фундаментальность, глубина. Якоб был глубоко обижен нападками брата. Его раздражительность усиливалась тяжелым заболеванием.

Спор велся в резких тонах, сопровождался взаимными насмешками. В 1695г. Якоб предал спор гласности в «Acta Eruditorum», выступил против брата с нападками. В 1697г. Через 4 года редакция журнала заявила, что отказывается предоставить место для продолжения дискуссии. Но и это не остановило братьев: конец спора наступил со смертью Якоба. Только много лет спустя Иоганн признал свои ошибки.

Последние годы жизни Якоба омрачались «изнурительной лихорадкой, высасывающей здоровье по каплям». Этими словами один из биографов Бернулли выразительно описывает состояние туберкулезного больного. 16 августа 1705г. Якоб Бернулли скончался. По желанию покойного на его памятнике высечено изображение спирали с надписью: eadem mutate resurgo (измененная, я возвращаюсь прежней).

Собрание сочинений Якоба Бернулли вышло в 1744г. Его «Искусство предположений» издал племянник Николай I в Базеле в 1713г.; четвертая часть «Искусства предположений», содержащая теорему Бернулли, переведена на русский язык ﴾ 2 ﴿

2.4.Неравенство Бернулли

Рассмотрим формулу системы геометрической прогрессии

При q>1 все слагаемые в левой части равенства, начиная со второго, больше 1, поэтому сумма больше n, а при 0<q<1 эта сумма меньше n. Таким образом,

> n при q>1

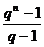< n при 0<q<1

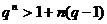После умножения этих неравенств на , получим(при q>1) неравенство . Откуда (1)

(при q=1 неравенство (1) обращается в равенство).

Из (1) при получаем неравенство

(2)

Называемое неравенством Бернулли (знаменитое семейство швейцарских математиков).

Равенство (2) достигается при n=1 или при x=0 ﴾ 4 ﴿

Пример 1. Докажите неравенство

Решение. Достаточно представить 2=1+1 и применить (2):

Пример 2. Докажите, что

Решение. Возведем обе части неравенства в степень n:

Последнее неравенство справедливо в силу (2) 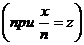, следовательно, верно и данное неравенство.

Пример 3. Верно ли числовое неравенство

Решение. Вынесем за скобки и сократим, затем применим неравенство из примера 2 при n=3 и. Получим

Данное числовое неравенство верно.

Пример 4. Найдите наименьшее значение функции 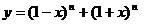на отрезке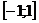

Решение. В силу неравенства Бернулли

Равенство достигается при x=0

Ответ: 2.

Пример 5. Доказать, что если у арифметической прогрессии 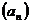и геометрической прогрессии с положительными членами и 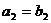, то все последующие члены геометрической прогрессии больше соответствующих членов арифметической прогрессии.

Решение. Из условия следует, что , где - разность арифметической прогрессии, а - знаменатель геометрической прогрессии. Отсюда . В формуле общего члена геометрической прогрессии применим неравенство (2)

 

 

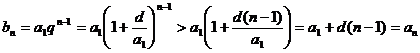
Огюстен Коши

 

 

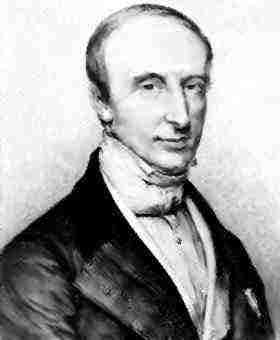Огюстен Коши родился 21 августа 1789г. в Париже в семье видного чиновника. Его отец был ревностный католик и роялист. В начале с Коши занимался его отец, прекрасный лингвист, а в 1805г. Огюстен поступил в Политехническую школу, затем в 1807г.- в Школу мостов и дорог, которую окончил в 1810г. Лагранж отметил выдающиеся математические способности юноши и предсказал ему блестящее будущее. После окончания инженерной школы Коши получил ответственное поручение по постройке военного порта в Шербуре. Здесь в 1811г. он написал свой первый мемуар о многогранниках, где решил некоторые вопросы, не поддававшиеся первоклассным математикам. Затем последовали еще мемуары по теории многогранников, о симметрических функциях, алгебраических уравнениях, по теории чисел. В 1816г. Коши представил на конкурс Парижской академии наук знаменитое исследование по теории волн на поверхности тяжелой жидкости и получил премию. В этом же году он был назначен правительством членом Института Франции. Тогда же началась интенсивная преподавательская деятельность Коши: с 1816г. он профессор Политехнической школы, в 1816-1830гг.- Сорбонны, в 1848-1857гг.- Колледж де Франс. Им написаны "Курс анализа" (1821г.), "Резюме лекций, прочитанных в Королевской политехнической школе" (1823г.), "Лекции о приложении анализа к геометрии" (1826-1828). В этих курсах Коши дал определение непрерывности функции, построил строгую теорию сходящихся рядов, ввел определенный интеграл как предел интегральных сумм. Вся система анализа построена на базе предела. Книги Коши долгое время служили образцом для курса анализа. Революция 1830г. и изгнание Карла X резко изменили судьбу Коши: не считая возможным изменить присяге Карла X, он отказался присягнуть правительству Луи Филиппа, потерял должности и вынужден был покинуть Францию. Некоторое время он провел в Швейцарии, затем получил место в Туринском университете на кафедре математической физики. Карл X, поселившийся в Праге, пригласил Коши в 1832г. в качестве учителя и воспитателя сына. Коши несколько лет путешествовал с ним по Европе. Так было до 1838г. Коши предлагали различные должности, но он отказывался от них, руководствуясь своими католическими и роялистическими убеждениями. Во Франции и в Институт он вернулся в 1838г. Революция 1848г. отменила присягу, и Коши получил кафедру в Колледже де Франс, где и проработал до самой смерти. Умер Коши 22 мая 1857г. ДОСТИЖЕНИЯ В МАТЕМАТИКЕ. Коши принадлежит определение определенного интеграла. Неопределенный интеграл Коши ввел как частный случай определенного, при переменном верхнем предел. Он доказал непрерывность такого интеграла по верхнему пределу, а также доказал справедливость формулы Ньютона-Лейбница. Кроме того, Коши исследовал несобственный интеграл. ﴾ 5 ﴿

Неравенство Коши

Теорема 1. Для неотрицательных чисел 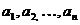справедливо неравенство Коши

(3)

Равенство (3) достигается тогда и только тогда, когда

Доказательство. Пусть числа - положительны. Положим 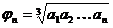. Это число называется средним геометрическим положительных чисел при (при полагаем по определению ).

Очевидно, что имеют место равенства

Применим неравенство (1), полагая в нем (4)

Отсюда при любом получим неравенства

Складывая эти неравенства почленно, получим

Перенесем 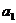налево, разделим неравенство на и получим (3).

Равенство (3) достигается, когда все 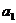равны, что следует из неравенства (4). В нем равенство достигается тогда, когда . Отсюда следует .

Заметим что неравенство (3) справедливо для неотрицательных чисел

Это знаменитое неравенство, принадлежащее французскому математику О. Коши, было опубликовано в 1821 г. Его доказательство занимало несколько

страниц сложных выкладок и основано на методе математической индукции. С тех пор появилось несколько десятков различных доказательств этого неравенства.

Рассмотрим несколько примеров применения (3) ﴾ 4 ﴿

Пример 6. Произведение положительных чисел 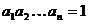. Докажите, что

Утверждение следует из неравенства Коши.

Пример 7. Сумма положительных чисел . Докажите, что при

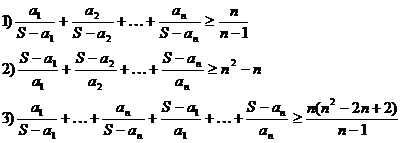
Решение. Каждое слагаемое в 1) представим в виде

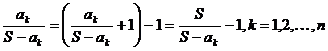
Сложим равенств и применим дважды неравенство (3)

Чтобы доказать 2), дважды применим неравенство (3)

Наконец, сложив 2) и 1) получим 3).

Пример 8. Найдите наименьшее значение суммы

Решение. Достаточно применить (1) для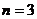

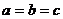Значение достигается, когда и, следовательно, является наименьшим.

Пример 9. Решите уравнение

Решение. Ясно, что стандартное решение этого уравнения ведет к большим трудностям, поэтому попробуем иначе. Очевидно при правая часть уравнения равна 2, а при меньше 2, поскольку каждое слагаемое меньше. Итак, правая часть не превосходит 2. Левую часть представим в виде

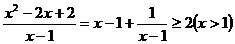
В силу неравенства Коши для двух чисел, причем равенство достигается при , т.е. при .

Следовательно, уравнение имеет единственный корень .

Пример 10. При каких значениях 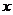функция

достигает на отрезке наибольшего значения?

Решение. Запишем функцию в виде

Сумма сомножителей. Стоящих в скобках, равна 8, и в силу неравенства Коши для имеем

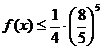
Следовательно, 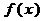достигает наибольшего значения, когда , т.е. при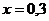

Пример 11. Найдите наибольшее и наименьшее значение функции

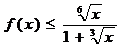
Решение. Область определения – промежуток

- наименьшее значение, т.к.

В силу неравенства Коши имеем

Причем равенство достигается при , то есть . Видим, что наибольшее значение функции.

Из примеров видно, как можно применять неравенства Бернулли и Коши при решении задач на отыскание наибольших и наименьших значений функций. В таких задачах обычно применяется производная, однако в ряде случаев они проще решаются с помощью неравенств Бернулли и Коши. ﴾ 4 ﴿

 

Христиан Гюйгенс

 

Голландский механик, физик и математик, создатель волновой теории света Христиан Гюйгенс ван Зюйлихем родился в Гааге в богатой и знатной семье крупного политического деятеля. Учился в университетах Лейдена (1645-1647) и Бреды (1647-1649), где изучал юридические науки и математику. В 1665-1681 гг. жил и работал в Париже, с 1681 г. – в Гааге. Первый иностранный член Лондонского королевского общества (с 1663).

Научную деятельность Гюйгенс начал в 22 года, опубликовав работу об определении длины дуг окружности, эллипса и гиперболы (1651). В 1654 г. появилась его работа «Об определении величины окружности», явившаяся важнейшим вкладом в теорию определения отношения окружности к диаметру (вычисление числа π). Затем последовали другие значительные математические трактаты по исследованию циклоиды, логарифмической и цепной линии и др. Его трактат «О расчётах при игре в кости» (1657) – одно из первых исследований в области теории вероятностей. Гюйгенс совместно с Робертом Гуком установил постоянные точки термометра – точку таяния льда и точку кипения воды. В эти же годы Гюйгенс работает над усовершенствованием объективов астрономических труб, стремясь увеличить их светосилу и устранить хроматическую аберрацию. С их помощью Гюйгенс открыл в 1655 г. спутник планеты Сатурн (Титан), определил период его обращения и установил, что Сатурн окружен тонким кольцом, нигде к нему не прилегающим и наклонным к эклиптике. Все наблюдения приведены Гюйгенсом в классической работе «Система Сатурна» (1659). В этой же работе Гюйгенс дал первое описание туманности в созвездии Ориона и сообщил о полосах на поверхностях Юпитера и Марса.

Астрономические наблюдения требовали точного и удобного измерения времени. В 1657 г. Гюйгенс изобрёл первые маятниковые часы, снабженные спусковым механизмом; своё изобретение он описал в работе «Маятниковые часы» (1658). Второе, расширенное издание этой работы вышло в 1673 г. в Париже. В первых 4 частях её Гюйгенс исследовал ряд проблем, связанных с движением маятника. Он дал решение задачи о нахождении центра качания физического маятника – первой в истории механики задачи о движении системы связанных материальных точек в заданном силовом поле. В этой же работе Гюйгенс установил таутохронность движения по циклоиде и, разработав теорию эволют плоских кривых, доказал, что эволюта циклоиды есть также циклоида, но по-другому расположенная относительно осей.

В 1665 г., при основании Французской АН, Гюйгенс был приглашен в Париж в качестве её председателя, где и прожил почти безвыездно 16 лет (1665-1681). В 1680 г. Гюйгенс работал над созданием «планетной машины» – прообраза современного планетария, – для конструкции которой разработал достаточно полную теорию цепных, или непрерывных, дробей. Это – последняя работа, выполненная им в Париже.В 1681 г., вернувшись на родину, Гюйгенс снова занялся оптическими работами. В 1681-1687 гг. он производил шлифовку объективов с огромным фокусными расстояниями в 37, 54, 63 м. Тогда же Гюйгенс сконструировал окуляр, носящий его имя, который применяется до сих пор. Весь цикл оптических работ Гюйгенса завершается знаменитым «Трактатом о свете» (1690). В нём впервые в совершенно отчётливой форме излагается и применяется к объяснению оптических явлений волновая теория света. В главе 5 «Трактата о свете» Гюйгенс дал объяснение явления двойного лучепреломления, открытого в кристаллах исландского шпата; классическая теория преломления в оптически одноосных кристаллах до сих пор излагается на основе этой главы.К «Трактату о свете» Гюйгенс добавил в виде приложения рассуждение «О причинах тяжести», в котором он близко подошёл к открытию закона всемирного тяготения. В своём последнем трактате «Космотеорос» (1698), опубликованном посмертно, Гюйгенс основывается на теории о множественности миров и их обитаемости. В 1717 г. трактат был переведён на русский язык по приказанию Петра I. ﴾ 6 ﴿

Неравенство Гюйгенса

Покажем, как можно из неравенства Коши получить одно важное неравенство, носящее имя Х. Гюйгенса.

Теорема 2. Для любых положительных чисел верно неравенство

(5)

Действительно, неравенство вытекает из тождества

Применяем неравенство (3) к каждому из двух слагаемых в скобках

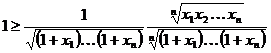
Умножим это неравенство на знаменатель, возведем в степень и получим (5).

Равенство (5) достигается, когда все 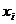равны. Это вытекает из условия равенства (3).

Неравенство (5) имеет место и для неотрицательных .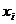

Полагая, получим неравенство

(6)

Заметим, что равенство (6) достигается при

Если в неравенстве (6) числа удовлетворяют условию , то

Отсюда получаем известное неравенство

Отметим еще частный случай неравенства (6). При

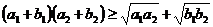(7) ﴾ 4 ﴿

Пример. Найдите наименьшее значение функции

Решение. Запишем функцию 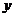в виде, удобном для применения неравенства Гюйгенса

Следовательно, наименьшее значение функции равно 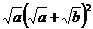и достигается при условии , т.е. при ﴾4﴿