2014-02-03
914
Рис.35
Проведем через центр масс С тела произвольные оси Cx'y'z', а через любую точку О на оси Сх' - оси Oxyz, такие, что Оy ½½ Сy', Oz ½½ Cz' (рис. 35). Расстояние между осями Cz' и Оz обозначим через d. Тогда
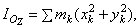
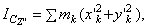
но, как видно из рисунка, для любой точки тела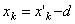 
или 
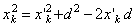, а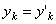 
. Подставляя эти значения 
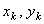, в выражение для 
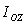и вынося общие множители d 2 и 2d за скобки, получим
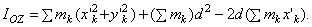
В правой части равенства первая сумма равна Icz', а вторая - массе тела М. Найдем значение третьей суммы. На основании формул для координат центра масс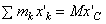 
.Так как в нашем случае точка С является началом координат, то x C = 0 и, следовательно, 
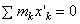. Окончательно получаем:
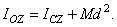
Формула выражает следующую теорему Гюйгенса:
Момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями.
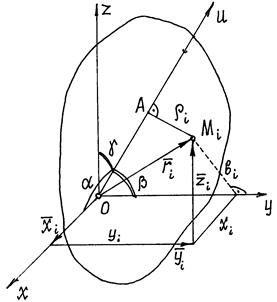
Найдем момент инерции тела относительно оси u, проходящей через некоторую точку О (рис. 36).
