Определение стоимости и доходности векселей, облигаций и акций

Рассмотрим в первую очередь стоимость и доходность краткосрочных ценных бумаг (векселей, депозитных и сберегательных сертификатов).

Векселя. Пусть N - цена погашения векселя, который выписан на t дней. По какой цене должен продаваться вексель? Другими словами, какова должна быть стоимость векселя?

Если считать, что цена погашения N - наращенная сумма, то ее современная величина (используем простые проценты)

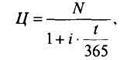
следовательно, стоимость векселя или сертификата составляет Ц.

Обратим внимание на то, что если ценная бумага выписана в пользу банка, то банк рассчитывает ее стоимость с использованием антисипативной процентной ставки. Для банка стоимость векселя или сертификата

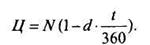
Проанализируем доходность операций с векселями или сертификатами. Под доходностью будем понимать относительный доход держателя ценной бумаги за время владения, выраженный в годовой процентной ставке. Пусть владелец купил бумагу за t₁ дней до погашения и за t ₂ дней до погашения продал ее (t₁ > t₂). Определим его доход. Обозначим через t₁ и t₂ депозитные процентные ставки, действовавшие соответственно за t₁ и t₂ дней до погашения. Тогда цены покупки Ц₁ и продажи Ц₂ вычисляются следующим образом:

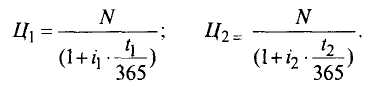
Владелец держал вексель (t₁ - t₂) дней, поэтому цены покупки и продажи связаны следующим соотношением:

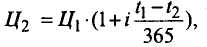
где i - годовая доходность владельца, отсюда

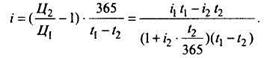
Чтобы доход i был больше нуля, необходимо выполнение условия i₁t₁ > i₂t₂ Пусть в моменты покупки и продажи векселя или сертификата действует одна депозитная ставка (i_o = i₁ = i ₂), тогда

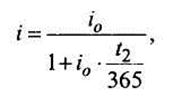
откуда следует, что максимальный доход можно получить, если не продавать вексель до его погашения.

При определении стоимости и доходности облигаций необходимо в зависимости от способа получения дохода рассмотреть различные виды облигаций:

• с фиксированной купонной ставкой, погашаемые в конце их срока по номиналу;

• с нулевым купоном, реализуемые с дисконтом и погашаемые в конце срока по номиналу;

• с равномерно возрастающей купонной ставкой, погашаемые по номиналу в конце срока;

• типа "французская рента", доход по которым выплачивается до тех пор, пока они находятся у держателя. Доходность облигаций определяется тремя показателями:

1) купонной нормой доходности (процентной ставкой, указанной на купоне);

2) текущей нормой доходности (отношением купонного дохода к цене приобретения);

3) полной нормой доходности (доходностью от полного использования облигации: получение процентов, их капитализация и получение номинала).

Облигации с фиксированной купонной ставкой. При определении их стоимости применима модель постоянной ограниченной ренты, в которой главный член ренты R =g • N (g - купонный процент; N - номинал облигации). Кроме того, необходимо учесть приведенную сумму погашения облигации. Тогда стоимость облигации

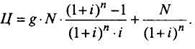
Если же выплаты начисляются и производятся т раз в год по годовой ставке j, то

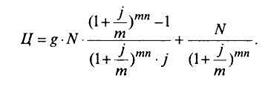
Купонная норма доходности облигации равна g. Текущая норма доходности i_T= 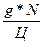. Вычислим полную норму доходности облигации.

При этом поступим аналогично тому, как поступили при определении доходности краткосрочных ценных бумаг. Предположим, что облигация куплена по цене Ц' за t₁ лет до погашения и за t₂ лет до погашения продана по цене Ц".

Для Ц' и Ц "имеем следующее соотношение:

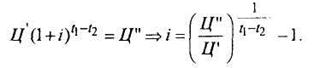
Если учесть, что стоимости Ц' и Ц" определялись теоретически в соответствии с формулой расчета стоимости, то после подстановки и соответствующих преобразований получим:

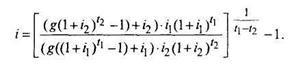
Предположим теперь, что t₂ = 0, т.е. облигация владельцем не продавалась, а была погашена в срок, тогда доходность ее

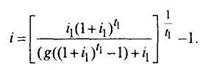
В этом случае доходность i называется доходностью к погашению. Очевидно, что доходность имеет место, когда выражение в квадратных скобках и в степени больше 1.

Облигации с нулевым купоном. Эти облигации продаются с дисконтом, их стоимость

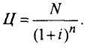
Купонная и текущая нормы доходности облигаций с нулевым купоном равны нулю, так как g = 0. Полную норму доходности определим аналогично предыдущему:

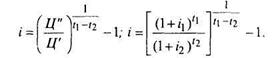
Доход получается, если выполняется неравенство

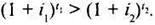
Если банковская депозитная ставка i₁ не меняется со временем (i₁ = i₂), то доход будет всегда. Предположим, что t₂ = 0, т. е. облигация находилась у владельца до погашения, тогда i = i₁ (доход от облигации с нулевым купоном равен банковской депозитной ставке).

Облигации с равномерно возрастающей купонной ставкой. При определении стоимости такой облигации используем модель переменной ренты с постоянным приростом платежей, при этом R=g*N, E = g'*N (g' - прирост купонной ставки g за период). Тогда стоимость облигации

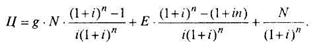
Купонная доходность для п- гопериода составляет g + g'(n- 1). Текущая доходность:

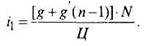
Полная норма доходности

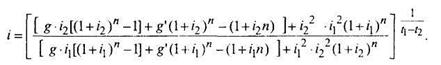
Облигации типа "французская рента". При оценке этих облигаций используется модель постоянной вечной ренты. Модели оценки этих облигаций аналогичны моделям оценки облигаций с фиксированной купонной ставкой. Отличие состоит лишь в "продолжительности жизни" - для облигаций типа "французская рента" п стремится к бесконечности. Тогда стоимость этих облигаций

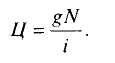
Если выплаты производятся Р раз в год, то стоимость

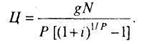
Купонная норма доходности - g.

Текущая норма доходности

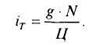
Полная норма доходности рассчитывается из выражения

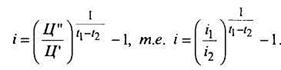
Доходность имеется, если i₁ > i ₂, откуда следует вывод: это происходит, когда облигация куплена по банковской ставке i₁ большей, чем банковская ставка i₂ при продаже. Заметим также, что цены покупки и продажи имеют обратную зависимость от банковской ставки.

Акции. Поскольку срок действия акции не ограничен, предположив, что дивиденд за каждый год является постоянным и равным Д в абсолютном выражении, можно для определения стоимости акций использовать модель вечной ренты. В этой модели член ренты R = Д, тогда стоимость акций

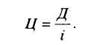
При оценке стоимости акций используется понятие курса акций, который находится как отношение стоимости акции к номиналу:

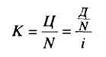
либо в долях единицы, либо в процентах (в этом случае обе части равенства необходимо умножить на 100%). В литературе существует путаница в использовании понятия "курс акций", связанная с двояким представлением дивиденда (в абсолютном и в процентном выражении). Следует помнить, что дивиденд всегда определяется в абсолютном (денежном) выражении, его же процентное выражение получается от сопоставления абсолютного значения дивиденда с номиналом.

При рассмотрении понятия "стоимость акций" имелась в виду расчетная стоимость. Кроме расчетной стоимости акция обладает также:

• номинальной стоимостью (номиналом);

• курсовой стоимостью, которая служит ее рыночной стоимостью или ценой на бирже;

• бухгалтерской (книжной) балансовой стоимостью. Номинал - стоимость акции, указанная при ее эмиссии (имеются в виду акции номинального типа).

Курсовая, или рыночная, стоимость акций оценивается различным образом, по различным формулам. Один из способов ее вычисления исходит из предположения о существовании двух типов инвесторов. Одни ориентируются на высокое дивидендное покрытие, другие - на прирост стоимости акций. Согласно этому рыночная цена акций определяется как средневзвешенная сумма:

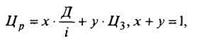
где х - доля инвесторов, надеющихся на высокие дивиденды;

у - доля инвесторов, рассчитывающих на дальнейшее увеличение курсовой стоимости акций;

Ц₃ - цена закрытия данного вида акций на прошедших торгах.

В зависимости от величины х и у при определении рыночной цены акций преобладает курсовой (у ≈ 1) или дивидендный (х ≈ 1) подход. Очевидно, что ни курсовой, ни дивидендный подходы не могут дать удовлетворительную оценку реальной цены акций.

Рыночную цену акций будущих периодов рассчитывают с помощью методов технического анализа, согласно которым по статистике изменения курсовой стоимости акции в предыдущие периоды прогнозируют ее изменение в будущем.

Балансовая стоимость акций представляет собой отношение объемов (руб.) чистых активов акционерного общества к количеству оплаченных акций. К чистым активам акционерного общества относятся основные средства, нематериальные активы, оборотные средства минус долги общества (расчеты с кредиторами, заемные средства, доходы будущих периодов). Балансовая стоимость рассчитывается один раз в год после закрытия годового баланса. Часто при расчете рыночной цены акции используют ее балансовую стоимость.

Доходность акций вычисляется аналогично доходности облигаций. Выделяют три показателя доходности:

1) дивидендная норма доходности (дивиденд в процентном по отношению к номиналу выражении);

2) текущая норма доходности (отношение дивиденда к цене приобретения)

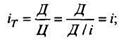
она представляет собой величину кредитной банковской ставки;

3) полная норма доходности, или доходность от владения акцией в течение временного периода ∆t. Предположив, что ∆t - кратно целому числу лет, воспользуемся уже знакомым соотношением между ценой покупки Ц₁ и ценой продажи Ц₂:

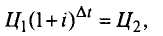
тогда

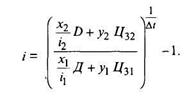
Доходность будет тогда, когда только выражение в скобках будет больше единицы.

Рассмотрим случай, когда имеется инвестор, ориентирующийся только на дивиденды и не учитывающий изменения рыночной цены акции, т.е. х₁ = х₂ = 1,

у₁= у₂ = 0. Здесь доходность будет выше нуля, если i₁ > i₂, т.е. доходность наблюдается при понижающейся банковской ставке, конечно же, в предположении постоянных дивидендов.

Поскольку акции являются "вечными" ценными бумагами с величиной дивидендов, изменяющейся во времени произвольным образом, возникают сложности в разработке моделей оценки их стоимости и доходности в аналитическом виде. Именно этим объясняются большие разночтения в трактовке понятий стоимости и доходности акций.

Сейчас единодушно принимается всеми специалистами только выражение для курса акций. Сложности в разработке моделей доходности для акций возникают еще и в связи со следующим обстоятельством. Как отмечалось ранее, полная норма доходности акций зависит от трех переменных: величины дивидендов, ссудной банковской ставки и цены продажи акции. Все три переменные в случае с акциями выступают величинами неопределенными, в то время как у облигаций неопределенна только величина ссудного процента (номинал и купон известны).

Отсутствие моделей для расчета стоимости и доходности акций с переменным дивидендом, депозитной ставкой процента и рыночной стоимостью акций не превращает ситуацию в безнадежную. Модели с постоянным дивидендом и банковской ставкой могут успешно применяться для оценки акций с переменным дивидендом и банковской ставкой, если использовать дивиденды и банковские ставки, средние за оцениваемый временной период.

Воздействие инфляции. В условиях инфляции необходимо учитывать влияние фактора изменения покупательной способности денег на стоимость и доходность ценных бумаг. Предположим, что h - темп прироста инфляции, выраженный в виде долей единицы, тогда (1 + h) - годовой рост инфляции.

Годовая реальная ставка i_p определяется из равенства

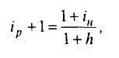
где i_Н - номинальная годовая ставка.

Имеем

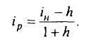
Попытаемся изменить левую и правую части равенства так, чтобы в левой части оказалась величина i_н для сохранения же равенства в правой части умножим i_H на неизвестный коэффициент z, который можно определить из уравнения

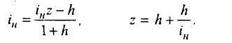
Введем ставку, обозначенную через r = i_н • z, тогда

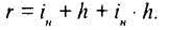
Ставку r принято называть брутто-ставкой, она учитывает инфляцию. Для того чтобы ввести учет инфляции во всех предыдущих формулах, вместо ставок i должна быть брутто-ставка r.

Определим брутто-ставку по простым процентам r_н:

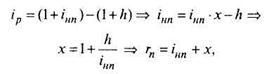
где i_нп - номинальная ставка простых процентов.

Брутто-ставка по простым процентам равна сумме номинальной ставки и темпа прироста инфляции, а брутто-ставка по сложным процентам - сумме номинальной ставки и темпа прироста инфляции, увеличенной на их произведение.