Портфель облигаций. Иммунизация портфеля облигаций

Инвестиционный портфель может быть составлен не только из акций, но и из облигаций. Особенность облигаций но сравнению с акциями состоит в том, что все денежные выплаты, которые порождает облигация, гарантированы, а рыночная стоимость облигаций жестко зависит от действующих в стране процентных ставок. При повышении процентных ставок стоимость облигаций снижается, при понижении процентных ставок стоимость облигаций повышается. Поэтому инвестиционный портфель облигаций подвержен процентному риску, связанному с изменением действующих процентных ставок.

Для описания процентного риска портфеля облигаций используется показатель дюрации Макколи, характеризующий чувствительность стоимости облигации к изменению процентных ставок.

Рыночная стоимость облигаций

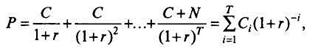
где С - ежегодная купонная выплата;

r - внутренняя норма доходности облигации, в нашем случае равная доходности

облигации до погашения;

N - номинал облигации;

T - срок погашения;

Рассмотрим первую производную стоимости облигации

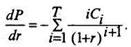
Умножим обе части равенства на (1 + r) / P, получим

Заметим, что левая часть этого равенства является эластичностью цены облигации по отношению к (1 + r) и характеризует процентное изменение цены облигации по сравнению с процентным изменением (1 + r). Преобразуем правую часть равенства. Обозначим через w_i отношение приведенной стоимости i -го платежа к текущей стоимости облигации, тогда

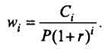
Из равенства

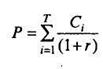
следует, что

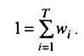
Таким образом, коэффициент w_i является долей цены облигации, которую вносит i -й платеж. Теперь можно произвести преобразование:

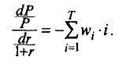
Полученная формула свидетельствует о равенстве эластичности цены облигации средневзвешенному времени погашения облигации. В данном случае дюрация Макколи определяется как

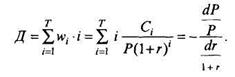
Дюрация Д представляет собой этастичность цены облигации по процентной ставке, поэтому она может быть использована как мера риска изменения цены облигации при изменении процентной ставки.

Дюрация бескупонной облигации равна времени ее погашения, а дюрация купонной облигации всегда меньше времени ее погашения. Следовательно, на равное изменение процентных ставок при равных сроках погашения более реагирует цена бескупонной облигации, чем цена купонной.

Дюрацию можно измерять и в годах, и в купонных периодах. Величина дюрации в годах может быть равна величине дюрации в купонных периодах, поделенной на количество купонных периодов в году.

Поскольку дюрация характеризует риск облигации, связанный с изменением процентных ставок, то можно, используя дюрацию, управлять риском облигации или портфеля облигаций. Существует теорема об иммунитете Самуэльсона, согласно которой риск, связанный с изменением процентных ставок, можно хеджировать, выравнивая дюрации активов и задолженностей.

Например, предположим, что фирма должна заплатить 1 000 000 руб. через год. Возможно, для этого в будущем ей придется взять кредит, и если в течение года процентные ставки вырастут, то фирме придется заплатить повышенный процент за кредит. Для защиты фирмы от изменения процентных ставок можно уже сегодня создать актив с дюрацией, совпадающей с задолженностью. Дюрация задолженности равна одному году. Для защиты от изменения процентных ставок фирма может купить бескупонную облигацию с погашением через год и номиналом 1 000 000 руб. За эту облигацию фирма заплатит 1 000 000 / (1+r₁), где r₁ - годовая процентная ставка. Дюрация этой облигации равна году. Через год фирма получит по облигации 1 000 000 руб. и проведет платеж, при этом изменение процентных ставок никак не отразится на доходах фирмы в связи с проведенными операциями. Так с помощью бескупонной облигации была иммунизирована задолженность фирмы.

Величина дюрации облигации с изменением срока, оставшегося до погашения, изменяется, и связано это со следующими обстоятельствами.

Для купонной облигации общий риск от изменения процентных ставок имеет две составляющие: первая связана с изменением рыночной цены облигации, этот риск описывается дюрацией; вторая - с изменением процентной ставки, под которую реинтвестируются купонные платежи. Направления изменений этих составляющих риска противоположны. Так, при росте процентных ставок инвестор проигрывает в цене облигации, но выигрывает в связи с реинвестированием купонных платежей; при снижении процентных ставок наблюдается обратное. Существует точка во времени (в течение срока жизни облигации), когда эти два процесса уравновешивают друг друга и общая доходность облигации остается неизменной. Такая точка и определяется величиной дюрации облигации, рассчитанной в момент покупки облигации.

Например, инвестор купил купонную облигацию с доходностью до погашения 40% годовых с погашением через семь лет, дюрация облигации в момент покупки составляет пять лет. Это значит, что если инвестор продаст такую облигацию через пять лет, то доходность от проведенной операции составит 40% годовых. Если же он продаст облигацию раньше или позже пяти лет, то доходность может оказаться ниже. С учетом этих обстоятельств можно формировать соответствующую стратегию управления портфелем облигаций.

Вопросы для самопроверки

1. Почему используется "порфельный" подход к инвестированию?

2. Какие виды портфельных рисков существуют, чем они обусловлены и как можно с ними бороться?

3. В чем состоит различие эффективного и оптимального портфелей?

4. Что такое диверсификация?

5. Что такое хеджирование?

6. Что такое иммунизация?

7. Какие позиции по срочным контрактам необходимо открыть, чтобы захеджировать портфель акций?

8. Что такое дюрация?

9. Как защитить портфель облигаций от процентного риска?