Структурный метод

Для расчета различных систем автоматического управления их обычно разбивают на отдельные элементы, динамическими характеристиками которых являются дифференциальные уравне­ния не выше второго порядка. Причем различные по своей физиче­ской природе элементы могут описываться одинаковыми диффе­ренциальными уравнениями, поэтому их относят к определенным классам, называемым типовыми звеньями.

Изображение системы в виде совокупности типовых звеньев с указанием связей между ними называется структурной схемой. Она может быть получена на основе как дифференциальных урав­нений, так и передаточных функций. Данный способ и составляет суть структурного метода, т. е. метода представления систем ав­томатического управления различной физической природы.

Хотя структурный метод не предлагает новых способов расчета, он позволяет наглядно представить взаимосвязь элементов систе­мы и оценить при наличии соответствующего опыта отдельные свойства переходных и статических процессов. Он настолько ши­роко используется в практике проектирования, что, по существу, может считаться одним из «языков», на котором обсуждаются свойства систем автоматического управления.

Рассмотрим подробнее отдельные типовые звенья и их различ­ные динамические характеристики.

3.1. ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ

3.1.1. Пропорциональное (усилительное) звено

Пропорциональным называется звено, поведение которого опи­сывает алгебраическое уравнение

y =ku,

где k - коэффициент усиления. Строго говоря, это звено не являет­ся динамическим, но относится к типовым.

Примерами таких звеньев могут служить безынерционные усилители. механические редукторы, многие датчики сигналов и т. д. передаточная функция звена следующая:

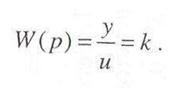
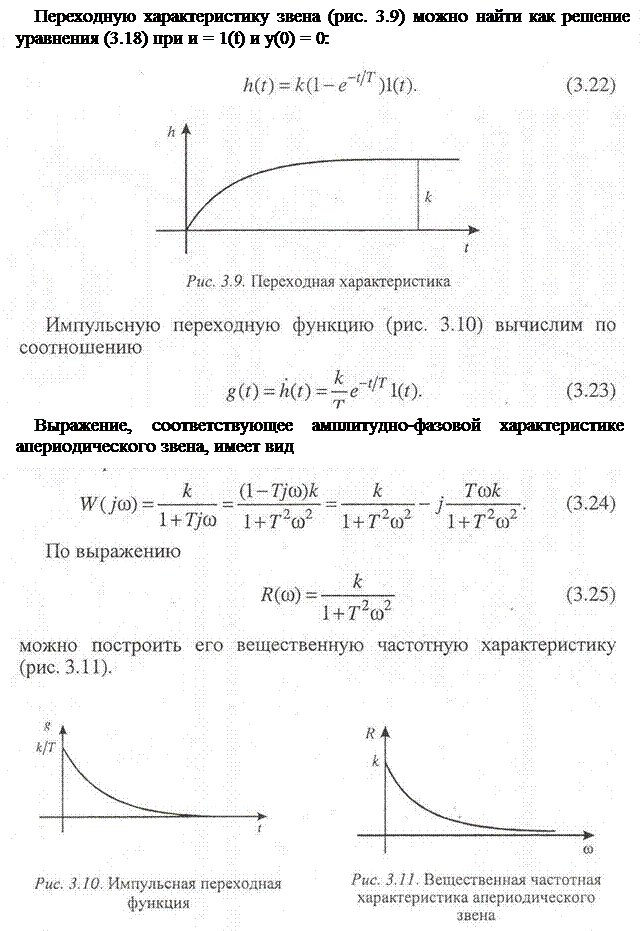
Переходная характеристика (реакция звена на скачкообразное входное воздействие 1(t)) имеет вид

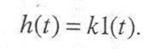
Импульсная переходная функция пропорционального звена оп­ределяется выражением

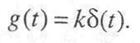
Модальные характеристики (собственные значения и собствен­ные векторы) для него отсутствуют.

Заменив в передаточной функции р на jω, получим выражения
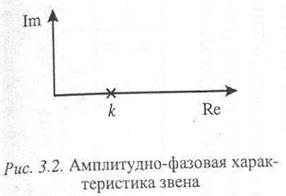
для частотных характеристик. Амплитудно-фазовая характеристика представляет собой точку на комплексной плоскости в соответствии с формулой

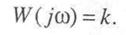
Вещественная частотная характеристика определяется соотношением (рис. 3.1)

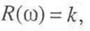
а мнимая частотная характеристи­ка отсутствует (I(ω)=0).

Амплитудная частотная характеристика может быть построена по соотношению

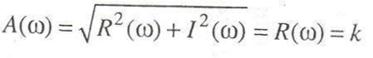
и имеет тот же вид, что и ВЧХ. Выражение для ФЧХ следующее:

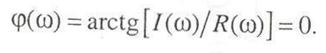
Таким образом, при прохождении через пропорциональное звено амплитуда периодического входного сигнала изменяется в k раз, а базовый сдвиг отсутствует.

Амплитудно-фазовая характеристика звена имеет вид точки на комплексной плоскости (рис. 3.2).

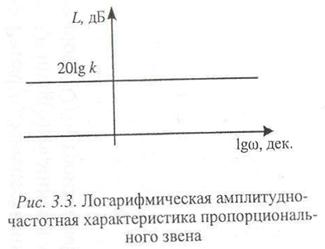
Логарифмическая АЧХ звена представляет собой прямую, па­раллельную оси абсцисс:

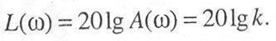
Как следует из выражений (3.3, 3.4) и рис. 3.3, пропорциональ­ное звено пропускает входные сигналы без искажений.

3.1.2. Дифференцирующее звено

Дифференцирующим называется звено, которое описывается дифференциальным уравнением

y =ku.

Его передаточная функция имеет вид

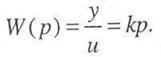
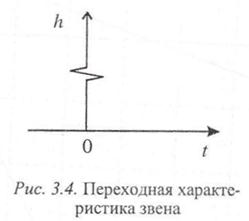
Примером дифференцирующего звена часто может служить тахогенератор постоянного тока. Переходная характеристика диффе­ренцирующего звена определяется выражением

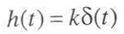
и имеет вид 5 -функции (рис. 3.4).

Импульсная переходная функция (рис. 3.5) представляет собой «дуплет» δ –функций

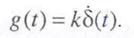
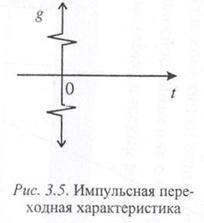
Рассмотрим теперь частотные характеристики звена. Ампли­тудно-фазовая характеристика

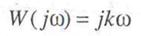
совпадает с положительной мнимой полуосью комплексной плос­кости; вещественная частотная характеристика равна нулю, Л(ц>) = 0; мнимая частотная характеристика соответствует выра­жжению

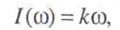
т. е. представляет собой линейно нарастающую функцию. С ней совпадает амплитудная частотная характеристика, которая имеет вид

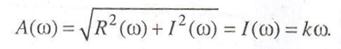
Фазовую частотную характеристику можно определить по со­отношению

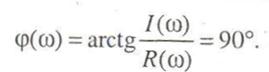
Следовательно, на всех частотах имеется постоянный фазовый сдвиг.

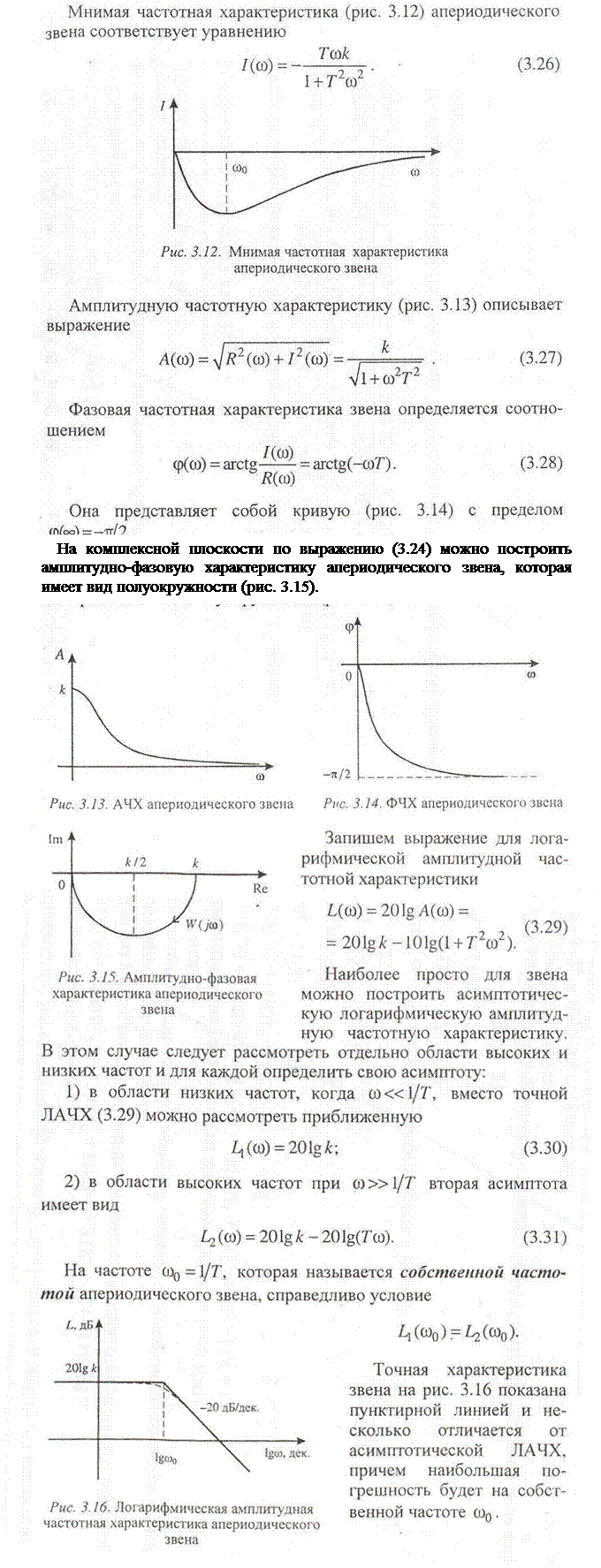
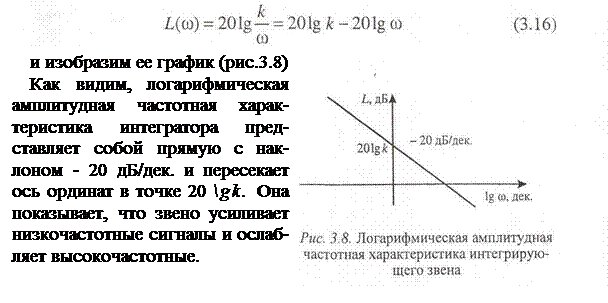
Причем се можно получить, исследуя отдельно области низких _и высоких частот или суммируя ЛАЧХ пропорционального и дифференцирующего звеньев.

Нетрудно убедиться, сравнивая выражения (3.28) и (3.29) с выражениями (3.37) и (3.38), в том, что логарифмические ампли­тудная и фазовая частотные характеристики форсирующего звена представляют собой зеркальное отображение относительно оси абсцисс соответствующих логарифмических характеристик апе­риодического звена.

Передаточную функцию звена получим на основе символиче­ской записи дифференциального уравнения

Передаточную функцию звена получим на основе символиче­ской записи дифференциального уравнения

		Для определения модальных характеристик запишем характери­стическое уравнение звена