Из теории вероятности известно, что оценкой математического ожидания является среднее арифметическое результатов отдельных наблюдений - 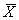
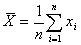 , (3.4)
, (3.4)
где 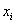 - i-й результат наблюдения;
- i-й результат наблюдения;
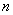 - число результатов наблюдений.
- число результатов наблюдений.
Оценка дисперсии ряда наблюдений 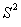 рассчитывается по формуле
рассчитывается по формуле
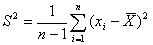 . (3.5)
. (3.5)
Среднее квадратическое отклонение ряда наблюдений 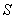 является основной характеристикой размера случайных погрешностей результатов наблюдений. Формула для расчета о ценки среднего квадратического отклонения s
является основной характеристикой размера случайных погрешностей результатов наблюдений. Формула для расчета о ценки среднего квадратического отклонения s
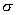 = +
= + 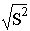 , (3.6)
, (3.6)
при n à 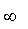 (практически при n > 30), S2 à Д, S à s.
(практически при n > 30), S2 à Д, S à s.
Дополнительную информацию по теме можно получить в [1-7,10].
4 Лекция 4. Погрешности измерений (продолжение)
Содержание лекции:
- оценка и учет погрешностей при точных и технических измерениях, аксиомы случайности и распределения; вероятностные оценки погрешности результата измерений на основании ряда наблюдений, методы повышения точности измерений и средств измерений.
Цель лекции:
- изучить вероятностные оценки погрешности результата измерений на основании ряда наблюдений: доверительные границы, доверительный интервал и доверительная вероятность; методы уменьшения случайных и систематических погрешностей измерений, методы повышения точности СИ.
4.1 Оценка и учет погрешностей при точных измерениях
Точные измерения должны проводиться так, чтобы не было систематических погрешностей. Теория случайных погрешностей базируется на двух аксиомах, основывающихся на опытных данных.
Аксиома случайности: при очень большом числе измерений случайные погрешности, равные по величине, но разные по знаку, встречаются одинаково часто: число отрицательных погрешностей равно числу положительных.
Аксиома распределения: малые погрешности случаются чаще, чем большие; очень большие погрешности не встречаются.
Полным описанием случайной величины, а следовательно и случайной погрешности, является закон распределения. Существуют различные законы распределения случайной величины. В практике измерений наиболее распространенными законами распределения случайных погрешностей являются нормальный и равномерный законы распределения.
4.1.1 Вероятностные оценки погрешности результата измерений на основании ряда наблюдений
Цель обработки результатов наблюдений – это установление действительного значения измеряемой величины, которое может быть принято вместо истинного значения измеряемой величины, и степени близости действительного значения к истинному.
Действительное значение неизбежно содержит случайную погрешность. Поэтому степень близости действительного значения к истинному значению нужно оценивать с позиции теории вероятности. Такой оценкой является доверительный интервал. Доверительный интервал случайной погрешности – это интервал, в который с заданной доверительной вероятностью попадают значения случайной погрешности. Доверительный интервал может быть установлен, если известны закон распределения случайной погрешности и характеристики этого закона (лекция 3).
Согласно ГОСТ 8.011 – 72, доверительный интервал – одна из основных форм выражения точности измерений. ГОСТ устанавливает следующую форму представления результата измерения
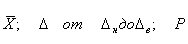 , (4.1)
, (4.1)
где 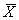 – результат измерения (среднее арифметическое значение);
– результат измерения (среднее арифметическое значение);
D, Dн, Dк – абсолютная погрешность измерения с нижней и верхней границами;
Р – доверительная вероятность, с которой погрешность находится в этих границах.
В теории вероятностей доказано, что для нормального закона распределения случайной погрешности, величина 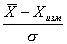 есть случайная величина
есть случайная величина 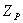 , распределенная по нормальному закону с МО = 0 и Д = 1; а величина
, распределенная по нормальному закону с МО = 0 и Д = 1; а величина 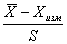 есть случайная величина
есть случайная величина 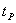 , распределенная по закону Стьюдента. Для
, распределенная по закону Стьюдента. Для 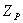 и
и 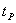 существуют таблицы, по которым можно найти их значения, определяющие с доверительной вероятностью Р границы доверительного интервала Dн, Dк для
существуют таблицы, по которым можно найти их значения, определяющие с доверительной вероятностью Р границы доверительного интервала Dн, Dк для 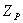 и
и 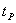 соответственно.
соответственно.
При 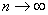 , S à s, т.е. с увеличением числа наблюдений
, S à s, т.е. с увеличением числа наблюдений 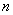 закон распределения Стьюдента приближается к нормальному. (Практически уже при n > 30
закон распределения Стьюдента приближается к нормальному. (Практически уже при n > 30 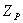 становится равным
становится равным 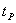 ).
).
В практике измерений применяют различные значения доверительной вероятности Р = 0,90; 0,95; 0,98; 0,99; 0,9973 и 0,999.
При нормальном законе распределения случайной погрешности часто пользуются доверительным интервалом от +3s до -3 s с доверительной вероятностью 0,9973. Данная доверительная вероятность означает, что в среднем из 370 случайных погрешностей только одна будет превышать значение = 3 s. Так как на практике число отдельных измерений редко больше нескольких десятков, то применяется «закон трех сигм»: все возможные случайные погрешности измерения, распределенные по нормальному закону, практически не превышают по абсолютному значению 3 s.
Конечная цель анализа выполненных измерений состоит в определении погрешности результата наблюдения ряда значений измеряемой величины 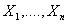 , погрешности их среднего арифметического значения, принимаемого за окончательный результат измерения, относительной частоты погрешностей и вероятности.
, погрешности их среднего арифметического значения, принимаемого за окончательный результат измерения, относительной частоты погрешностей и вероятности.
4.1.1.1 Оценка погрешности (точности) результата наблюдения
Оценкой точности результата наблюдения служит среднее квадратическое отклонение результата наблюдения - 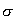 (лекция 3). Для получения полного представления о точности и надежности оценки случайного отклонения результата наблюдения должны быть указаны доверительные границы, доверительный интервал и доверительная вероятность. При известном
(лекция 3). Для получения полного представления о точности и надежности оценки случайного отклонения результата наблюдения должны быть указаны доверительные границы, доверительный интервал и доверительная вероятность. При известном 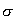 доверительные границы указываются следующим образом: нижняя граница (-
доверительные границы указываются следующим образом: нижняя граница (- 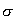 ), верхняя граница (+
), верхняя граница (+ 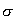 ) (сокращенно
) (сокращенно 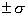 ), за пределы которых с вероятностью Р=0,683 (или 68,3%) не выйдут значения случайных отклонений (
), за пределы которых с вероятностью Р=0,683 (или 68,3%) не выйдут значения случайных отклонений ( 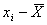 ). Доверительный интервал выражается в виде
). Доверительный интервал выражается в виде 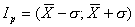 . В зависимости от целей измерения могут задаваться и другие доверительные границы
. В зависимости от целей измерения могут задаваться и другие доверительные границы 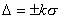 , а доверительный интервал погрешности результата наблюдений
, а доверительный интервал погрешности результата наблюдений
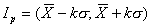 , (4.1)
, (4.1)
где 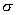 - среднее квадратическое отклонение результата наблюдения (3.6);
- среднее квадратическое отклонение результата наблюдения (3.6);
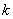 - квантильный множитель, значение которого зависит от выбранного закона распределения случайной погрешности.
- квантильный множитель, значение которого зависит от выбранного закона распределения случайной погрешности.
Так для равномерного закона распределения 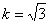 и не зависит от доверительной вероятности. Для нормального закона распределения
и не зависит от доверительной вероятности. Для нормального закона распределения 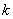 зависит от значения доверительной вероятности (Р) и количества выборочных значений (n): значения
зависит от значения доверительной вероятности (Р) и количества выборочных значений (n): значения 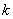 =
= 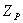 при n > 30;
при n > 30; 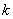 =
= 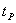 при n < 30 (закон Стьюдента). Значения
при n < 30 (закон Стьюдента). Значения 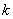 для наиболее употребительных доверительных вероятностей Р и различных n приведены в [8, Табл.П1-4-1].
для наиболее употребительных доверительных вероятностей Р и различных n приведены в [8, Табл.П1-4-1].
4.1.1.2 Оценка погрешности (точности) результата измерения
Результат измерения принимается равным среднему арифметическому значению 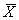 . Согласно теории погрешностей, оценка среднего квадратического отклонения результата измерения
. Согласно теории погрешностей, оценка среднего квадратического отклонения результата измерения 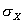 в
в 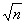 раз меньше оценки среднего квадратического отклонения результата наблюдений
раз меньше оценки среднего квадратического отклонения результата наблюдений
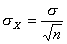 . (4.2)
. (4.2)
Доверительный интервал погрешности результата измерений
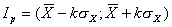 , (4.3)
, (4.3)
где 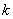 - имеет тот же смысл, что в формуле (4.1);
- имеет тот же смысл, что в формуле (4.1);
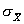 - среднее квадратическое отклонение результата измерения.
- среднее квадратическое отклонение результата измерения.
4.2 Оценка и учет погрешностей при технических измерениях
Технические измерения – измерения практически постоянных величин, выполняемых однократно с помощью рабочих средств измерений (лекция 2). Случайные погрешности в большинстве случаев не являются определяющими точность измерения, поэтому отпадает необходимость многократных измерений. За результат однократного измерения принимают показания средства измерения. Результирующая погрешность однократного измерения при применении измерительного показывающего прибора прямого действия может быть оценена приближенной максимальной (или предельной) погрешностью, определяемой по формуле
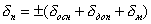 , (4.4)
, (4.4)
где 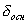 - пределы допускаемой основной погрешности применяемого измерительного прибора при его эксплуатации в нормальной области значений влияющих величин (НУ), %;
- пределы допускаемой основной погрешности применяемого измерительного прибора при его эксплуатации в нормальной области значений влияющих величин (НУ), %; 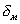 - методическая погрешность, %;
- методическая погрешность, %; 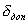 - пределы допускаемых дополнительных погрешностей измерительного прибора, %, определяемые отклонением влияющих величин за пределы, установленные для их нормальных значений или для нормальной области значений, согласно формуле
- пределы допускаемых дополнительных погрешностей измерительного прибора, %, определяемые отклонением влияющих величин за пределы, установленные для их нормальных значений или для нормальной области значений, согласно формуле
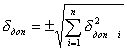 , (4.5)
, (4.5)
где 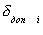 - значение предела допускаемой дополнительной погрешности измерительного прибора, вызванное отклонением i-ой влияющей величины, %.
- значение предела допускаемой дополнительной погрешности измерительного прибора, вызванное отклонением i-ой влияющей величины, %.
Чтобы точность технических измерений определялась только значением 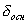 , необходимо исключить
, необходимо исключить 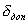 и
и 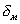 . Для этого нужно обеспечить правильную и тщательную установку СИ, создать условия работы, близкие к НУ.
. Для этого нужно обеспечить правильную и тщательную установку СИ, создать условия работы, близкие к НУ.
4.3 Методы повышения точности измерений и средств измерений
4.3.1 Методы уменьшения случайной погрешности измерений:
а) метод многократных измерений; увеличивая число измерений 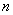 , теоретически можно сделать оценку
, теоретически можно сделать оценку 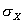 , согласно (4.2), которая определяет собой случайную погрешность, сколь угодно малой;
, согласно (4.2), которая определяет собой случайную погрешность, сколь угодно малой;
б) метод многоканальных измерений (использование параллельных измерений одной и той же физической величины); для этого необходимо использовать сразу несколько СИ и результаты наблюдений обрабатывать совместно.
4.3.2 Методы уменьшения систематической погрешности измерений:
а) устранение источников систематической погрешности до начала измерений;
б) методы исключения систематических погрешностей путем введения поправок по окончании измерений;
в) использование более точных СИ.
4.3.3 Методы повышения точности СИ: используются рассмотренные выше методы увеличения точности измерений: а) метод многократных измерений; б) метод многоканальных измерений;
в) метод параметрической стабилизации (конструкторско-технологический метод), который состоит в стабилизации статической характеристики СИ; параметрическая стабилизация реализуется путем изготовления СИ из точных и стабильных элементов, термостабилизации, экранировки СИ от магнитных и электрических полей и т.п.; данный метод уменьшает систематическую и случайную погрешности СИ;
г) структурные методы, которые основаны на том, что в состав СИ включаются дополнительные узлы, элементы и меры, обеспечивающие повышение точности этих СИ за счет информации, полученной с их помощью.
Дополнительную информацию по теме можно получить в [1,6,7,8,12,13,14].
5 Лекция 5. Основные сведения о средствах измерений
Содержание лекции:
- основные виды средств измерений (СИ); эталоны, образцовые и рабочие средства измерений и их классификация, статические характеристики измерительных устройств.
Цель лекции:
- изучить классификацию и определения различных видов средств измерений, статические характеристики СИ: функция преобразования, диапазон измерений, чувствительность, порог чувствительности.
Средства измерений (СИ) – технические средства, используемые при измерениях и имеющие нормированные метрологические характеристики.
Метрологические характеристики (МХ) – характеристики свойств СИ, оказывающие влияние на результаты и погрешности измерений.
Классификация средств измерений представлена в приложении Г на рисунке Г1.
Мера – СИ, предназначенное для воспроизведения физических величин заданного размера. Примеры - Гиря – мера массы; резистор – мера сопротивления; линейка- мера длины.
Измерительные устройства (ИУ) применяются самостоятельно или в составе измерительных установок или систем. В зависимости от формы представления информации измерительные устройства подразделяются на измерительные приборы (ИП) и измерительные преобразователи (ИПр).
Измерительный прибор – СИ, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. Измерительные приборы различают: 1) аналоговые и цифровые приборы; 2) показывающие и самопишущие приборы; 3) приборы прямого действия и приборы сравнения.
Измерительные преобразователи - СИ, предназначенные для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и (или) хранения, но не поддающейся непосредственному восприятию наблюдателем. Измерительные преобразователи бывают: первичные и вторичные; промежуточные и передающие.
Измерительные установки и системы – совокупность СИ, объединенных по функциональному признаку со вспомогательными устройствами, для измерения одной или нескольких ФВ объекта измерения.
Унифицированные СИ – СИ, входящие в ГСП (Государственную систему промышленных приборов и средств автоматизации). Эта система строится по блочно-модульному принципу:
- приборы с пневматическими входными и выходными сигналами 0,2 – 1 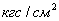 (0,02 – 0.1 МПа);
(0,02 – 0.1 МПа);
- приборы с электрическими входными и выходными сигналами:
а) постоянного тока 0-5, 0-20, 0-100 мА или 0-10 В;
б) переменного тока частотой 50 или 400 Гц; 1-0-1 В, 0-2 В, 1-3 В; 0-10 МГц, 10-0-10 МГц;
- приборы с электрическим частотным входным и выходным сигналами 1500 -2500 Гц и 4000 – 8000 Гц.
Эти приборы имеют унифицированные входные и выходные сигналы, что обеспечивает взаимозаменяемость средств измерений, способствует сокращению разновидности вторичных измерительных устройств, повышает надежность действия устройств автоматизации, дает широкие перспективы применения ЭВМ.
В зависимости от назначения СИ делятся на три категории:
а) рабочие меры, измерительные приборы, измерительные преобразователи;
б) образцовые рабочие меры, измерительные приборы, измерительные преобразователи;
в) эталоны.
Рабочие СИ – СИ, предназначенные для повседневных практических измерений во всех отраслях народного хозяйства. Различают рабочие СИ: 1) повышенной точности (лабораторные) СИ; 2) технические СИ.
Образцовые СИ – СИ, предназначенные для поверки и градуировки рабочих средств измерений. Верхний предел измерений образцовых СИ должен быть больше или равен верхнему пределу измерений поверяемого прибора. Допускаемая погрешность образцовых СИ должна быть значительно меньше (в 4-5 раз) допускаемой погрешности испытуемого прибора.
Рабочие СИ поверяются в контрольных лабораториях системы Госстандарта. Образцовые СИ поверяются в государственных контрольных лабораториях 1-го разряда по еще более точным образцовым мерам, приборам и преобразователям. Образцовые СИ 2-го разряда поверяются методом сравнения с образцовыми СИ 1-го разряда и т.д., образцовые СИ 1-го разряда поверяются в Государственных институтах мер и измерительных приборов по соответствующим рабочим эталонам.
Эталон – высокоточная мера, предназначенная для воспроизведения и хранения единицы величины с целью передачи ее размера другим СИ. От эталона единица ФВ передается разрядным эталонам, от разрядных эталонов – рабочим эталонам.
Различают эталоны:
- первичные;
- вторичные;
- рабочие (разрядные).
Первичный эталон – эталон, воспроизводящий единицу ФВ с наивысшей точностью, возможной в данной области измерений на современном уровне научно-технических достижений. Первичный эталон может быть национальным (государственным) и международным. Национальный эталон утверждается в качестве исходного СИ для страны национальным органом по метрологии.
Международные эталоны хранит и поддерживает Международное бюро мер и весов (МБМВ). Его задача состоит в систематических международных сличениях национальных эталонов разных стран с международными эталонами, а также и между собой. Сличению подлежат как эталоны основных величин системы СИ, так и производных величин. Установлены определенные периоды сличения: эталоны метра и килограмма – каждые 25 лет; электрические и световые эталоны – 1 раз в 3 года.
Вторичные эталоны – «эталоны-копии» сличаются с государственным эталоном и служат для передачи размера рабочим эталонам, а рабочие эталоны – эталонам более низкого разряда.
Самые первые эталоны официально были утверждены во Франции в 1799 году и переданы в Национальный архив Франции на хранение.
5.1 Статические характеристики измерительных устройств
Режим работы ИУ, при котором значения входных Х и выходных У сигналов не меняются, называется статическим (стационарным).
Статической характеристикой ИУ называется функциональная зависимость выходного сигнала от входного в статическом режиме работы указанного устройства (рисунок 5.1). В общем случае это нелинейная зависимость У = f(x).
Для ИУ с неименованной шкалой или шкалой, отградуированной в единицах, отличных от единиц измеряемой величины, статическую характеристику принято называть функцией преобразования. Для измерительных приборов статическую характеристику еще называют характеристикой шкалы. Определение статической характеристики связано с выполнением градуировки, поэтому для всех СИ используют понятие градировочной характеристики, под которой понимают зависимость между значениями величин на выходе и на входе СИ, составленную в виде таблицы, графика или формулы.
За исключением специальных случаев, основное требование, предъявляемое к статической характеристике ИУ, сводится к получению линейной зависимости между выходной и входной величинами. На практике это требование реализуется с некоторой заранее принятой погрешностью.
Диапазон показаний – область шкалы, ограниченная конечным и начальным значениями шкалы.
Диапазон измерений (рабочая часть шкалы) – область значений измеряемой величины (на шкале), для которой нормированы допускаемые погрешности средств измерений:
(Хв – Хн; Ув – Ун),
где Ун, Хн – нижний предел диапазона измерений;
Ув, Хв –– верхний предел диапазона измерений.
Для количественной оценки влияния на выходной сигнал ИУ входного сигнала в произвольной точке статической характеристики служит предел отношения приращения DУ выходного сигнала к приращению DХ входного сигнала, когда DХ à 0, то есть производная в выбранной точке равна
S = 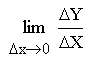 =
= 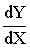 . (5.1)
. (5.1)
S – чувствительность ИП, определяется как отношение изменения сигнала на выходе ИП в вызвавшему его изменению измеряемой величины.
 У У    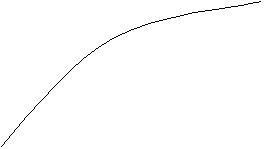 Ув Ув 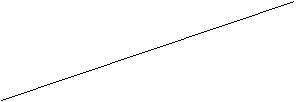 А 2 А 2  3 Ун 3 Ун   Х Хн Хв Х Хн Хв  диапазон измерения диапазон показаний диапазон измерения диапазон показаний  |
Рисунок 5.1 – Статическая характеристика измерительного устройства
Графически чувствительность – это тангенс угла наклона касательной к статической характеристике.
Если статическая характеристика - нелинейная, то его чувствительность будет различна в разных точках шкалы (шкала – неравномерная). СИ с линейной шкалой имеют равномерную шкалу и постоянное значение чувствительности.
У измерительных преобразователей статическая характеристика, как правило, линейная: 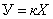 , где
, где 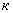 - коэффициент преобразования (передачи).
- коэффициент преобразования (передачи).
Цена деления – разность между двумя соседними отметками шкалы.
Порог чувствительности - это наименьшее изменение значения измеряемой величины х, способное вызвать уверенно фиксируемое изменение показания у измерительного прибора или выходного сигнала преобразователя.
Все рассмотренные выше характеристики СИ принято называть метрологическими, так как они влияют на точность осуществляемых с помощью этих устройств измерений.
СИ допускаются к применению только в том случае, если установлены нормы на их метрологические характеристики – нормированные метрологические характеристики (НМХ). Сведения о НМХ приводятся в технической документации на СИ.
Дополнительную информацию по теме можно получить в [5,8,9].
6 Лекция 6. Основные метрологические характеристики средств измерений
Содержание лекции:
- класс точности, классификация погрешностей измерительных приборов и измерительных преобразователей.
Цель лекции:
- изучить основные метрологические характеристики СИ: класс точности и погрешности СИ, их расчет и представление.
Метрологические характеристики (МХ) – характеристики свойств СИ, оказывающие влияние на результаты и погрешности измерений.
6.1 Класс точности и допускаемые погрешности
Класс точности – обобщенная метрологическая характеристика (МХ), определяемая пределами основной и дополнительных допускаемых погрешностей, а также другими свойствами средств измерений, влияющими на точность. Класс точности - величина безразмерная.
Пределы допускаемых основной и дополнительных погрешностей устанавливаются в стандартах на отдельные виды средств измерений (СИ).
Средствам измерений присваивают классы точности, выбираемые из ряда (ГОСТ 136-68) (1; 1.5; 2.0; 2.5; 3.0; 4.0; 5.0; 6.0) 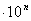 ; n = 1; 0; -1; -2;…
; n = 1; 0; -1; -2;…
Конкретные классы точности устанавливаются в стандартах на отдельные виды СИ. Чем меньше число, обозначающее класс точности, тем меньше пределы допускаемой основной погрешности.
Классы точности, нормируемые по приведенным погрешностям, имеют связь с конкретным значением предела погрешности, т.е. класс точности численно равен значению приведенной погрешности, выраженному в процентах.
СИ с двумя или более диапазонами (или шкалами) могут иметь два или более класса точности.
6.2 Погрешности измерительных устройств
Классификация погрешностей СИ представлена на рисунке Д1 (Приложение Д):
а) от характера проявления: систематические и случайные составляющие погрешности ИУ имеют тот же смысл, что и систематические и случайные погрешности измерений (лекция 3);
б) от условий применения:
1) основная погрешность СИ - погрешность СИ, используемого в нормальных условиях (Н.У.). Под Н.У. применения СИ понимаются условия, при которых влияющие величины (температура окружающего воздуха, барометрическое давление, влажность, напряжение питания, частота тока и т.д.) имеют нормальные значения или находятся в пределах нормальной области значений, а также определенное пространственное их положение, отсутствие вибрации, внешнего электромагнитного поля, кроме земного магнитного поля. Н.У. обычно не являются рабочими условиями применения СИ;
2) под пределом допускаемой дополнительной погрешности понимается наибольшая дополнительная погрешность, вызываемая изменением влияющей величины в пределах расширенной области значений (РОЗ), при которой средство измерений может быть признано годным и допущено к применению. В стандартах или технических условиях для каждого вида СИ устанавливают расширенную область значений влияющих величин, в пределах которой значение дополнительной погрешности не должно превышать установленных пределов. Терминам основная и дополнительная погрешности соответствуют фактические погрешности СИ, имеющие место при данных условиях;
в) от режима применения:
1) статическая погрешность – погрешность СИ, возникающая при использовании его для измерения постоянной величины;
2) динамическая погрешность – погрешность СИ, возникшая при использовании его для измерения переменной во времени величины;
г) от формы представления.
Для измерительного прибора и измерительного преобразователя определение абсолютной, относительной и приведенной погрешностей специфично. У измерительного прибора имеется шкала, отградуированная в единицах входной величины, либо шкала, отградуированная в условных единицах с известным множителем, поэтому результат измерения представляется в единицах входной величины. Это обуславливает простоту определения погрешности измерительного прибора. У измерительного преобразователя результаты измерений представляются в единицах выходной величины. Поэтому различают погрешности измерительного преобразователя по входу и по выходу.
Абсолютная погрешность измерительного прибора – разность между показаниями прибора и действительным значением измеряемой величиной
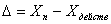 , (6.1)
, (6.1)
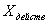 определяется с помощью образцового прибора или воспроизводится мерой.
определяется с помощью образцового прибора или воспроизводится мерой.
Относительная погрешность измерительного прибора – отношение абсолютной погрешности измерительного прибора к действительному значению измеряемой величины
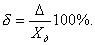 (6.2)
(6.2)
Приведенная погрешность измерительного прибора - отношение абсолютной погрешности измерительного прибора к нормирующему значению измеряемой величины
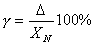 . (6.3)
. (6.3)
В качестве нормирующего значения используется верхний предел измерения или диапазон измерений измерительного прибора.
При определении погрешностей измерительного преобразователя (ИПр) известны следующие величины: 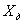 - действительное значение величины на входе Ипр, которое воспроизводится мерой или определяется с помощью образцового СИ на входе.
- действительное значение величины на входе Ипр, которое воспроизводится мерой или определяется с помощью образцового СИ на входе. 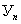 - значение величины на выходе Ипр, определяется с помощью образцового средства на выходе;
- значение величины на выходе Ипр, определяется с помощью образцового средства на выходе; 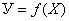 - функция преобразования измерительного преобразователя;
- функция преобразования измерительного преобразователя; 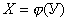 - обратная функция преобразования измерительного преобразователя.
- обратная функция преобразования измерительного преобразователя.
Абсолютная погрешность измерительного преобразователя по выходу – разностьмежду действительным значением величины на выходе измерительного преобразователя, отображающей измеряемую величину, и значением величины на выходе, определяемым по действительному значению величины на входе с помощью градуировочной характеристики, приписанной измерительному преобразователю
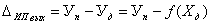 , (6.4)
, (6.4)
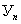 ,
, 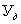 определяются при одном значении входной величины.
определяются при одном значении входной величины.
Абсолютная погрешность измерительного преобразователя по входу – разностьмежду значением величины на входе измерительного преобразователя, определяемым по действительному значению величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и действительным значением величины на входе преобразователя
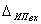 =
= 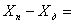
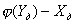 . (6.5)
. (6.5)
 2015-06-04
2015-06-04 2530
2530
