2014-02-02
725
Пример
Пример
; 
;
; 
.
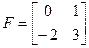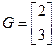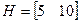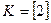Решение:
.
; 
;
; 
.
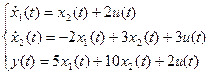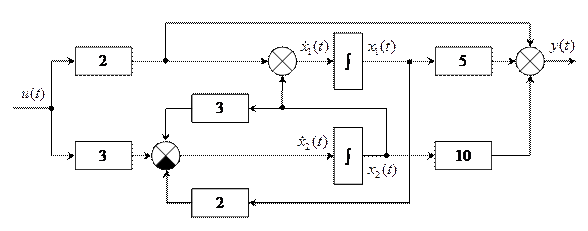
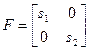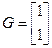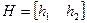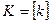Решение:
.
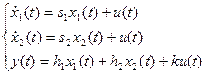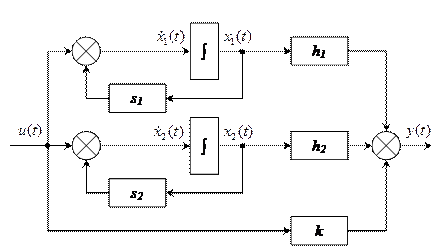
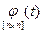– переходная матрица системы.
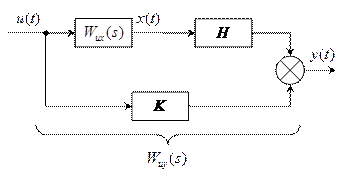
Пусть система задана в векторно-матричной форме:
‚
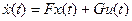
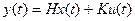и пусть для всех компонентов системы и процессов протекающих в ней
;
;
;
.
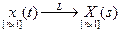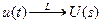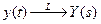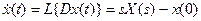Уравнения и ‚ в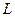 
-образах:
;
;
;
;
;
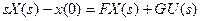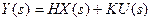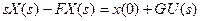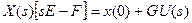
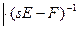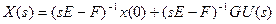Введем обозначение:
;
; ƒ
‚ ;
;
; „
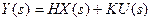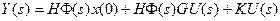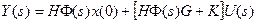Пусть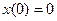 
– нулевые начальные условия
;
;
;
;
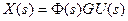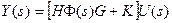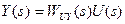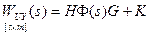– матрично-передаточная функция, задающая преобразования входных сигналов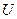 
в выходные сигналы 
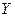, размерность которой 
.
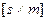При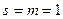 
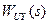– скалярная передаточная функция. В общем случае это матрица, элементы которой задают преобразования соответствующего входного сигнала в соответствующий выходной сигнал.
;
;
;
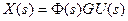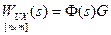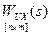– задает преобразования входных сигналов в компоненты вектора состояния.
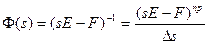, где
;
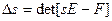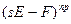– присоединенная матрица.
Если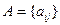 
, то 
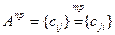, где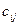 
– алгебраическое дополнение элемента 
матрицы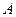 
.
Используя обратное преобразование Лапласа и теорему о свертке получим решение уравнения ƒ и „ относительно вектора состояния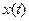 
и управляемых процессов 
.
|
|
|
;
; …
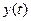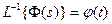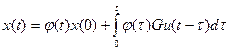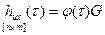; – матричная весовая функция.
; †
.
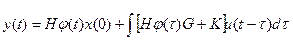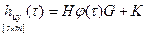Рассмотрим свободную составляющую
.
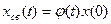Матрица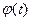 
показывает по какой траектории система переходит из произвольного начального условия 
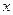в точке 0 в конечное.
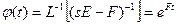– матричная экспонента.
