Методы расчета фундаментальной матрицы
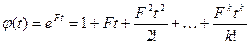 – ряд Фурье
– ряд Фурье- Использование операторного метода
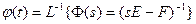 ;
;
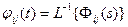 ;
;  .
.
Пример (вычисление фундаментальной матрицы)
Пусть задана система в виде:
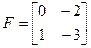 ;
; 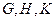 – произвольные.
– произвольные.
Вычислить фундаментальную матрицу системы 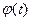 .
.
Решение:
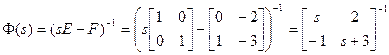 ;
;
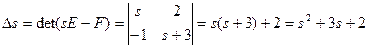 ;
;
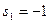 ;
; 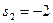 ;
;
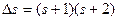 ;
;
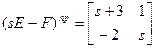 ;
;
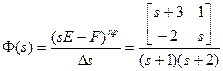 ;
;
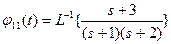
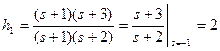 ;
;
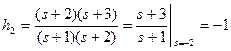 ;
;
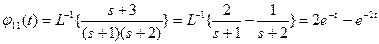 .
.
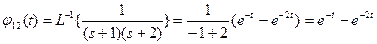 ;
;
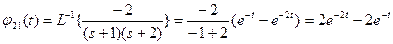 ;
;
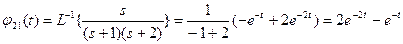 ;
;
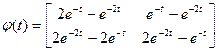 .
.
Элементы матрицы 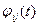 имеют вид, зависящий от корней характеристического уравнения
имеют вид, зависящий от корней характеристического уравнения 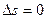 .
.
- Если корни характеристического уравнения простые (некратные, вещественные), то элемент
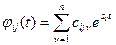 , где
, где
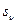 – корни характеристического уравнения;
– корни характеристического уравнения;
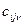 – числа, которые являются коэффициентами разложения на простые дроби элементов
– числа, которые являются коэффициентами разложения на простые дроби элементов 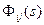 .
.
- Если корни характеристического уравнения комплексно-сопряженные, то
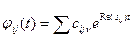 , где
, где
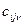 – гармоническая составляющая
– гармоническая составляющая
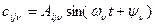 ;
;
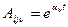 ;
;
 ;
;
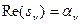 .
.
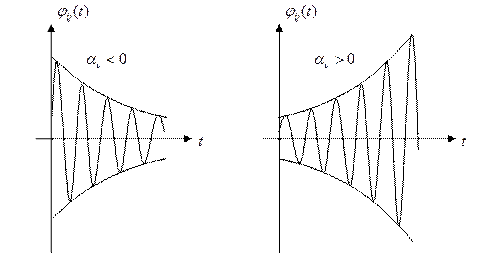
- Если корни вещественные, кратные
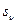 –
– 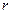 -ой кратности
-ой кратности
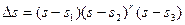 ;
; 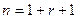 ;
;
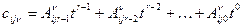 .
.
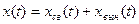 ;
;
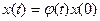 ;
;
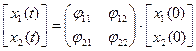 ;
;
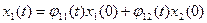 ;
;
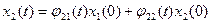 ;
;
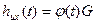 ;
;
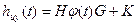 ; ‚
; ‚
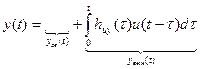 ;
;
Представление показывает, что матричная экспонента является матрицей, каждая компонента которой линейная комбинация скалярной экспоненты 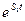 , а т.к. весовые матицы
, а т.к. весовые матицы 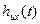 и
и 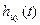 соответственно равны и ‚ также имеют своими компонентами линейные комбинации тех экспонент. Вид этих экспонент (затухающие или возрастающие) определяют траекторию движения системы
соответственно равны и ‚ также имеют своими компонентами линейные комбинации тех экспонент. Вид этих экспонент (затухающие или возрастающие) определяют траекторию движения системы 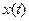 и
и 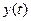 .
.
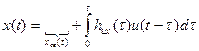 ;
;
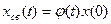 ;
;
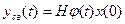 .
.
 2014-02-02
2014-02-02 797
797








