2014-02-02
2592
Практически любые линейные системы можно представить в виде различных комбинаций типовых элементарных звеньев. Для этого надо знать правило определения передаточных функций и отдельных звеньев.
Последовательное соединение звеньев – это когда выход предыдущего звена соединен со входом последующего звена.
 |
W(p)=W1(p)·W2(p)·…·Wn(p)
Параллельное соединение звеньев – когда вход общий, а выход алгебраически суммируется.
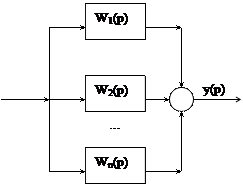
W(p)=W1(p)+W2(p)+…+Wn(p)
Соединение обратной связью – называют такое соединение, когда выход каждого элемента соединяется со входом каждого элемента.
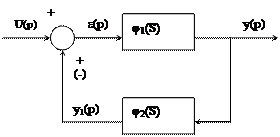
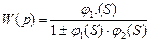
Передаточная функция соединения обратной связи равна дроби, числитель которой представляет собой передаточную функцию прямой части, а знаменатель передаточную функцию разомкнутой системы со знаком +, если обратная связь отрицательна, и со знаком -, если обратная связь положительна, увеличенная на единицу.
Пример:
написать передаточную функцию системы
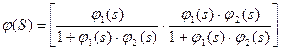
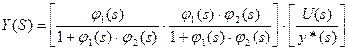
или
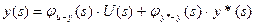
Для написания общих передаточных функций можно систему преобразовать к более простому виду. С этой целью можно пользоваться правилом переноса точки съема и правилом переноса точки суммирования.
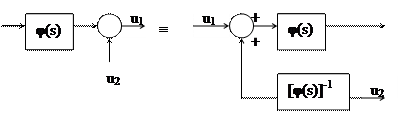
Правило переноса точки съема. Если точка съема переносится против направления сигнала, то в переносимую ветвь нужно включить элементы с передаточными функциями всех элементов, встречающихся на пути между прежней и новой точками съема.
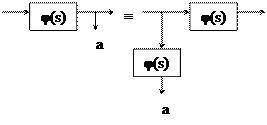
Если точка съема переносится по направлению прохождения сигнала, то в переносимую ветвь нужно включить элементы с обратными передаточными функциями всех элементов, встречающихся на пути между новой и прежней точками съема.
Правило переноса точки суммирования. Если точка суммирования переносится по направлению прохождения сигнала, то в переносимую ветвь нужно включить элементы с передаточными функциями всех элементов, встречающихся на пути между прежней и новой точками суммирования.
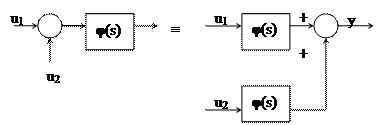
Если точка суммирования переносится против направления сигнала, то в переносимую ветвь нужно включить элементы с обратными передаточными функциями всех элементов, встречающихся на пути между новой и прежней точками съема.
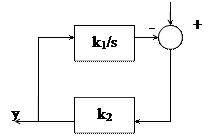
Пример:
найти передаточную функцию системы
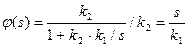
т.е.
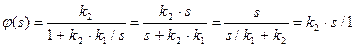- схема не явного обращения функции, т.к. операция дифференцирования - операция не корректная, то ее нужно осуществить по данной схеме – свойство обратной связи.
