Условия устойчивости

1. 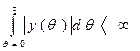- должна быть абсолютно интегрируема выходная величина.

2. Все корни характеристического уравнения должны быть левыми (отрицательными).

Примеры:

по критерию Гурвица

1. Определить устойчивость системы.

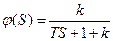, а₀>0

Заменяем Т=а₀, 1+k=а₁. Получаем матрицу Гурвица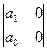

Если предполагаем, что а₀>0 и k>0, тогда система будет устойчивой.

Система с характеристическим уравнением 1-го порядка устойчива, если все его коэффициенты положительны.

2.

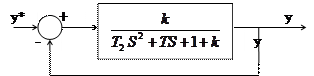
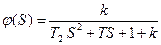. Заменяем T₂S²=a₀, TS=a₁, 1+k=a₂. Получим матрицу Гурвица .

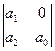Система будет устойчивой, если а₀>0, а₁>0 и k>0.

1. При каких соотношениях система устойчива.

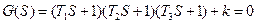. Заменяем T₁S+1=a₀, T₂S+1=a₁, T₃S+1=a₂, k=a₃.

Получим матрицу Гурвица .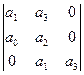

Отсюда соотношения

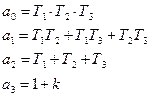
Система будет устойчивой, если а₀а₃<а₁а₂, k<k_гр=(1/Т₁+1/Т₂+1/Т₃)(Т₁+Т₂+Т₃)-1.

Для системы 3-го порядка должны выполняться соотношения между коэффициентами. Если k>k_гр, то система становится неустойчивой. При Т₁=Т₂=Т₃k_гр принимается минимально возможное значение =Δ.

Почему берем точку (-1; j0)?

Передаточная функция замкнутой системы 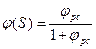. 1+φ_рс(S)=0, тогда φ_рс(S)=-1.

Примеры:

по критерию Найквиста.

1. Дана система

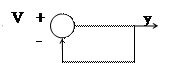
φ_р(S)=1, φ_р(jω)=1.

Годограф

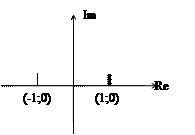
Система устойчива, т.к. не проходит через точку (-1; j0).

То же самое решим по критерию Михайлова.

Передаточная функция системы будет φ(S)=1/(1+1), G(S)=2, a₀=2.

1. Дана система

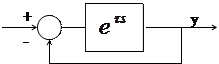
φ(S)=e^τs

Годограф

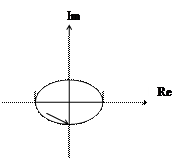
Система неустойчива т.к. проходит через точку (-1; j0).

3. Дана система

φ(S)=1/S

Годограф

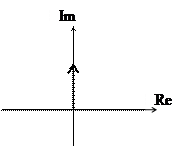
Система устойчива, т.к. коэффициенты положительны и уравнение 1-го порядка.