Вопросом выбора структуры параметров регулятора уделялось достаточно много времени. Большая часть из них основывается на экспериментах (настройки Копеловича, настройки Зингер-Николса).
Рассмотрим один из способов регулирования (Ротач, стр.15):
Рассматривается следующая система регулирования
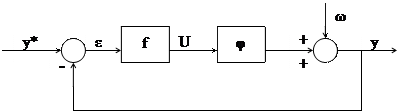
На основе теории статистических решений по среднеквадратическому критерию получим оптимальный оператор регулятора.
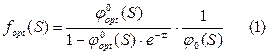 , где
, где
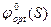 - оптимальный оператор системы без учета запаздывания;
- оптимальный оператор системы без учета запаздывания;
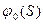 - оператор объекта без учета запаздывания.
- оператор объекта без учета запаздывания.
При регулировании промышленных объектов требуется, чтобы величина ошибки регулирования была существенно меньше отклонения регулируемой величины при отсутствии регулятора, такие системы называются системами высокой динамической точности. Частотная характеристика такой замкнутой системы равна 1, т.е.
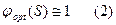
Кроме того, высокая точность только при малых значениях запаздывания (по отношению к спаду автокорреляционной функции приведенного воздействия). В этом случае оператор 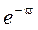 можно представить 2-мя 1-ми членами разложения ряда Тейлора
можно представить 2-мя 1-ми членами разложения ряда Тейлора
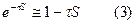
Подставляем (2) и (3) в (1), получаем
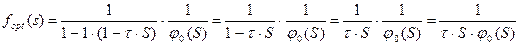
Для практической реализации применяется аппроксимация модели объекта в виде:
1. звена 2-го порядка 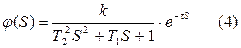
2. звена 1-го порядка, т.е. Т2=0
3. пропорциональное звено (безинерционное), т.е. Т2=0 Т1=0; для объектов самовыравнивания.
4. 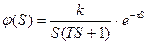
5. 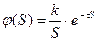
Подстановка этих аппроксимирующих выражений в (4) приводит к следующим типам законарегулирования, которые в частотное время реализуются в серийной аппаратуре и считаются типовыми:
- Пропорционально – интегрально – дифференциальный закон регулирования (ПИД - закон)
Его частотная характеристика определяется формулой
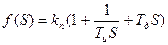 , где kп – коэффициент усиления пропорциональной части; Ти – постоянная интегрирования (время изодрома); Тд – постоянная дифференцирования; kп, Ти, Тд – настройки закона регулирования, которые связаны с аппроксимирующей характеристикой (1) следующим образом:
, где kп – коэффициент усиления пропорциональной части; Ти – постоянная интегрирования (время изодрома); Тд – постоянная дифференцирования; kп, Ти, Тд – настройки закона регулирования, которые связаны с аппроксимирующей характеристикой (1) следующим образом:

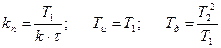 .
.
Регулятор с ПИД – алгоритмом осуществляет перемещение регулирующего органа по следующему закону:
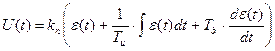 , где ε(t) – ошибка регулирования.
, где ε(t) – ошибка регулирования.
- Пропорционально – интегральный закон регулирования (ПИ - закон).
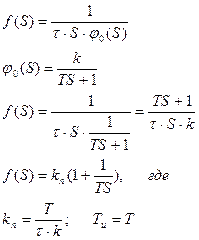
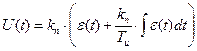
3. Пропорциональный закон регулирования (П - закон).
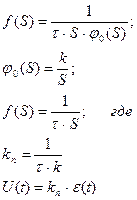
4. Пропорционально - дифференциальный закон регулирования (ПД - закон).
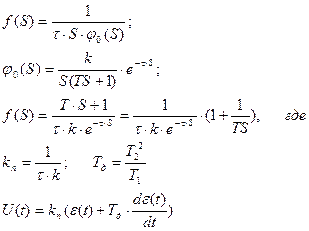
- Дифференциальный закон регулирования (Д - закон).
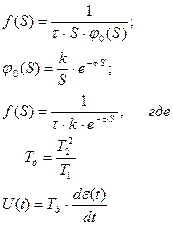
 2014-02-02
2014-02-02 913
913








