2014-02-02
613
Предварительно рассмотрим постановку задачи управления (Емельянов, Коровин). В задачу управления (стабилизации) можно сопоставить следующую схему:
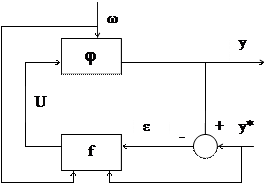
φ – оператор объекта;
f – оператор регулятора, который формирует из доступной ему информации (ε, ω, y*) управляющее воздействие U, при котором ε=y*-y=0 или лежит в допустимых пределах, т.е. цель сделать ε=0.
Охарактеризуем возможности, которыми функционирует ОУ для достижения цели. Как правило, специалист управления не имеет возможности влиять на внутреннее устройство ОУ, чтобы достичь y*=y. Поэтому единственная возможность влияния на воздействие связана с манипулируемым управляющим воздействием.
Здесь имеются только 2 «чистые» стратегии:
1. связана, с надлежащим формированием управляющего воздействия на основе имеющихся данных таким образом, чтобы последующее преобразование U объекта привело к требуемому результату y*=y.
Здесь к управляющему воздействию добавляется вспомогательный сигнал, соответствующий y*.
|
|
|
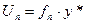
Для данной схемы 
.
При определенных условиях, в частности, если fп=φ-1, U=0, f2ω=0 получаем y*=y.
2. связана, с изменением оператора вход-выходного соответствия всей системы с помощью обратной связи.
U изменяется с помощью обратной связи по следующей схеме:
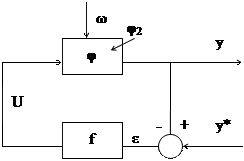
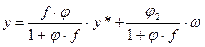
Из этого выражения видно, что обратная связь меняет оператор между входами y*· у и ω, (Если бы обратной связи не было, то получились бы другие операторы).
Более лучших результатов можно достигнуть с помощью комбинации прямой и обратной связи.
Пример:
Пусть ОУ описывается дифференциальным уравнением вида:
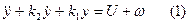, где k1 и k2 – постоянные коэффициенты.
Передаточная функция имеет следующий вид:
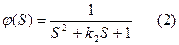
Пусть оператор прямой связи имеет передаточную функцию:
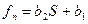, где b1 и b2 – постоянные коэффициенты, тогда
, тогда выход ОУ определяется из решения следующего дифференциального уравнения:
.
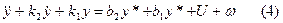(4) отличается от (1) дополнительными слагаемыми в правой части. Т.к. общее решение линейного дифференциального уравнения складывается из решения однородного и частного решения не однородного уравнения, то прямая связь влияет только на частное решение, т.е. на вынужденное движение и не оказывает никакого влияния на свободное движение. Если же использовать обратную связь с оператором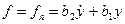 
, то дифференциальное уравнение замкнутой системы будет иметь следующий вид:
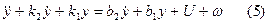
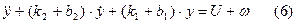
Из (6) следует, что обратная связь не изменяет правой части уравнения, но изменяет коэффициенты уравнения. Это означает, что обратная связь влияет как на свободное, так и на вынужденное решение. На основе этого примера покажем понятия статики и динамики системы управления.
|
|
|
Рассмотрим уравнение (1) при условии U≡0, ω=ω0 – const.
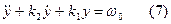
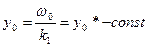. Это решение называется установившемся решением или статикойсистемы.
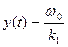- называется переходным процессом или динамикой системы.
Если в (7) k1 и k2>0, то компонента свободного движения затухает до 0 и объект колебательно или монотонно стремится к положению y0. Если используется прямая связь, то следует рассматривать уравнение (4) и при тех же условиях y*=const., U≡0, ω=ω0 – const. будем иметь:
.
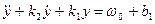В этом случае при k1 и k2>0 статика будет определяться выражением
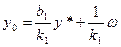. Отсюда видно, что прямая связь не влияет на динамику системы.
Определим зависимость между ε=y*-y0 (ошибка статики), получаем
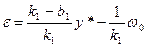- статическая ошибка системы. Поскольку коэффициент характеризует прямую связь, то он может использоваться для уменьшения статической ошибки.
Например, при b1 = k1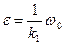 
.
Для обратной связи, при тех же предположениях имеем
.
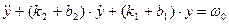В этом случае подбором коэффициентов обратной связи b1 и b2 замкнутую систему всегда можно сделать устойчивой:
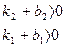
Следовательно, обратная связь меняет динамику системы. Но поскольку в установившемся состоянии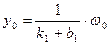 
, то статика так же зависит от обратной связи. В частности, увеличивается коэффициент b1 можно уменьшать статическую ошибку.
