Принципы построения линейных систем

1. принцип регулирования по нагрузке.

Простейшая задача управления, когда координатное управление отсутствует, т.е. ω≡0. В этом случае y=φU (1). Решение задачи дает программное управление, т.е.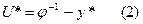

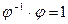- программное управление.

Поскольку y* характеризует «нагрузку», с которой работает объект, то этот принцип называется принципом регулирования по нагрузке.

Недостатки:

1. по физическому смыслу задачи оператор φ отражает реальный процесс, и поэтому должен удовлетворять условию физической осуществимости.

Пример:

Если φ(S)=1/S, тогда φ^-1=S.

В этом случае получается, что степень полинома числителя больше степени полинома знаменателя, а значит он не удовлетворяет принципу осуществимости. Поэтому речь может идти только о приближенной реализации этого оператора, а соответственно о приближенном решении программного управления.

2. задача управления не решается когда объект управления не устойчивый.

Пример:

Дано уравнение вида 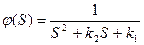или 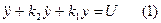, y≡0.

Система регулирования по нагрузке этого объекта имеет вид:

Если предположить, что обратный оператор реализуется точно, то возникает принципиальная трудность, например k₁<0. Это объясняется следующим, т.к. U*=φ^-1·y*=0, то на выходе объекта наблюдается только свободное движение, вызванное не нулевыми начальными условиями, тогда можно записать, что 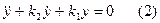, при k₁<0 характеристическое уравнение имеет один положительный корень и соответственно вся система не устойчива. Отсюда следует: если объект управления не устойчив, то задача управления по нагрузке не решается.

1. принцип управления по возмущению.

Пусть координатное возмущение (ω≡0) тождественно не равно 0, а объект можно представить в виде схемы:

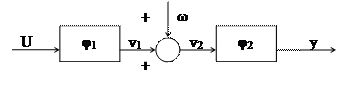
Определим φ: y= φ₁v₂; v₂=v₁+ω; v₁= φ₂U

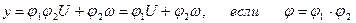
Если следовать принципу регулирования по нагрузке, то получим систему, выход которой определяется соотношением:

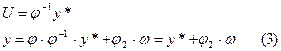
В случае, когда возмущения ω можно измерить, для устранения зависимости v от ω, следует применять принцип регулирования по возмущению. В соответствии с этим принципом, управление должно содержать компоненту компенсатора по возмущению, т.е. управление нужно взять в виде 2-х составляющих: 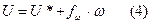, где f_ω – искомый оператор.

После подстановки (4) в , получим .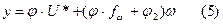

Из (5) видно, что задача управления решается точно, в том случае, когда y не зависит от ω, т.е. выполняется равенство: 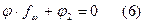, которое называется условием компенсации.

Из (6) получаем ;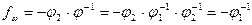

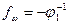- оператор регулятора по возмущению.

На основании этих формул можно представить структурную схему системы управления:

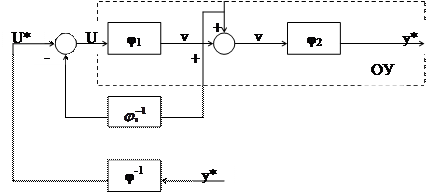
Недостатки:

1. Не устойчивые объекты управления не могут быть застабилизированы.

2. В общем случае оператор 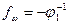- не осуществим физически, можно реализовать только приближенно.

3. Условие компенсации дается равенством 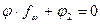. Малейшая погрешность в правой части ε приводит к тому, что зависимость объекта от ω не устраняется, получается .

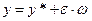4. Существенным ограничением принципа является предположение о возможности прямого и точного измерения системы.

Пример:

Дан ОУ вида 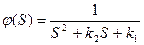с декомпозицией

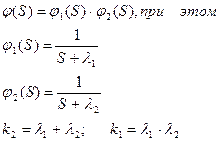
Надо: построить систему регулирования по нагрузке и возмущению.

По нагрузке

по возмущению

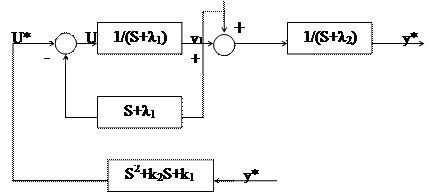Проведем анализ данной системы при условии, что в передаточной функции f_ω(S) допущена погрешность и в место нее используется передаточная функция

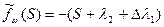, где Δλ₁ – маленькая величина.

Получим передаточную функцию ошибки регулирования:

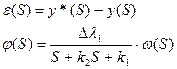
Поскольку ошибка регулирования выражается данной формулой, то при условии k₁=0 и k₂>0 получим 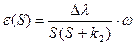, в котором 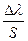- интегральная составляющая, а значит и ошибка может возрастать до бесконечности.

1. Принцип компенсации при косвенном измерении возмущения.

Поясним это следующей схемой:

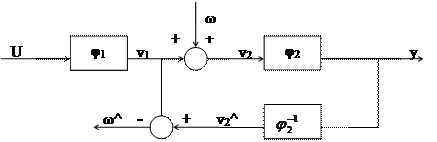
^ - оценка соответствующего воздействия.

Пусть измеряется входное воздействие у и внутренняя переменная v₁, тогда с помощью оператора v^₂, т.е. 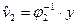, тогда

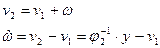, а далее можно применить принцип компенсации (заменяя v→v^) и сформировать управление в виде суммы 2-х компонент:

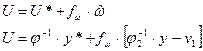
Этому выражению будет соответствовать следующая структурная схема:

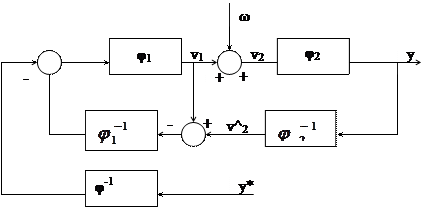
В этой схеме есть большой недостатки, т.к. в ней присутствует контур положительной обратной связи, оператор этого контура имеет вид:

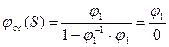. Возникает проблема деления на 0. Для ее решения вводят так называемый скрытый параметр.

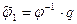, где q – оператор, которым пренебрегли при составлении ОУ, тогда

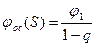, т.е получается, что свойство системы будет определяться не которыми не контролируемыми факторами (скрытыми параметрами q). Указанный недостаток не единственный для этой системы с компенсацией контролируемых возмущений:

· не устойчивые системы не могут быть застабилизированы;

· оператор 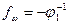физически не осуществим;

· должно в точности выполняться условие компенсации.

Пример:

Дан предыдущий пример с той же декомпозицией. Возмущение не контролируется. Построить систему регулирования и проанализировать анализ для контура положительной обратной связи.

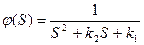
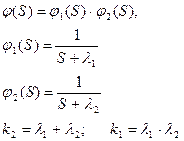
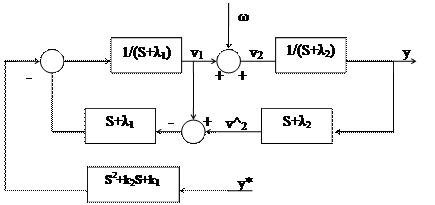
Выделим контур положительной обратной связи:

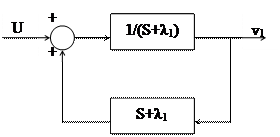
Передаточная функция ПОС:

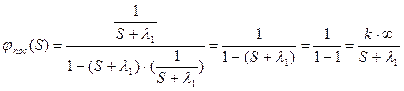, где k·∞ - бесконечный коэффициент усиления.

Из этого следует, что ПОС приводит к бесконечному коэффициенту усиления. Далее вместо оператора примем 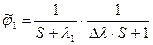, где Δλ – положительная маленькая величина.

Это означает, что первый множитель отражает медленные изменения, а 2-ой множитель быстрые изменения. С учетом этого, структурная схема контура положительной обратной связи будет иметь вид:

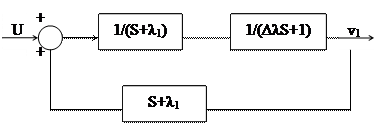
Передаточная функция этого контура будет иметь вид: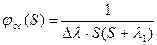

Характеристическое уравнение будет иметь 2 корня:

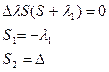
Решение характеристического уравнения имеет нулевой корень, а значит система находится на границе устойчивости и малейшее произвольно малое изменение коэффициентов приведет к не устойчивости.

Более тонкий подход к косвенному измерению возмущения используется принцип двухканальности Петрова.

1. Принцип двухканальности (принцип Петрова).

Достаточно эффективным методом синтеза компенсации возмущений является принцип двухканальности. Этот принцип является эвристическим (формально не выводимым) приемом структурного синтеза инвариантных систем (независимых от возмущений), в которых координаты не зависят от внешних независимых возмущений.

Как всякий эвристический прием он не имеет единственной последовательности действий и не приводит к однозначному решению. Центральной идеей этого принципа является: для достижения независимости регулируемой координаты системы от воздействий необходимо организовать еще один дополнительный канал влияния этого возмущения и настроить его таким образом, чтобы в заданной точке системы произошла взаимная компенсация сигналов, обусловленных действием возмущений.

1. Метод К – изображений.

Этот метод компенсации возмущений основан на точном знании моделей порождающих это возмущение. В линейной теории модель возмущения задается либо векторным уравнением 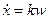, либо оператором, аннулирующим это возмущение .

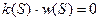Задание возмущения в том или ином виде этого удобства. В начале использовался только 1-ый способ задания, именно для него был (В.С. Кулебякиным) развит раздел в теории управления.

Эти два последние принципа имеют те же недостатки и поэтому, задача управления может быть решена приближенно. Для точного решения используется обратная связь.