2014-02-02
1133
Рис. 4.1 Переходные процессы в импульсной системе
Например, при kТ =1,5 в результате деления числителя выражения (4.3) на знаменатель получим:
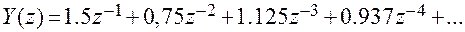
Коэффициенты этого ряда соответствуют ординатам колебательного переходного процесса на рис. 4.1 (кривая 3).
Пример. Определим для системы, рассмотренной в предыдущем примере, установившееся значение ошибки при ступенчатом и линейном воздействии.
Передаточная функция системы для сигнала ошибки
;
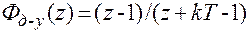Так как д.п.ф. рассматриваемого контура W (z) имеет полюс z =1, то при ступенчатом воздействии установившаяся ошибка равна нулю.
При линейном воздействии д (t)= at установившаяся ошибка
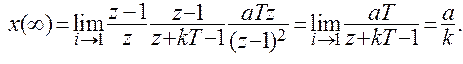
Перспективным направлением в технике автоматического управления является использование цифровых вычислительных машин в режиме ПЦУ. При осуществлении этого режима УВМ включают непосредственно в контур автоматической системы управления. УВМ функционирует в реальном масштабе времени и в темпе хода технологического процесса, вырабатывает управляющие воздействия, которые через исполнительные устройства передаются на управляемый объект. Одновременно УВМ выполняет функции задающего и сравнивающего устройства.
|
|
|
Рассмотрим типичную функциональную структуру одноконтурной цифровой системы управления (рис. 5.1, а). АЦП квантует непрерывный сигнал x по уровню и по времени и представляет его в цифровом коде. При этом образуется последовательность чисел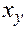 
, записанных в определенной (обычно двоичной) системе счисления. Цифровое вычислительное устройство ЦВУ в соответствии с заложенным в него алгоритмом выполняет над числами арифметические и логические операции и с периодом повторения Т выдает в виде числа управляющий сигнал 
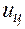. ЦАП состоит из декодирующего и фиксирующего устройств, которые из выходной последовательности чисел 
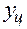формируют непрерывное управляющее воздействие 
.
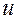Если непрерывная часть системы и алгоритм работы ЦВУ линейны, то рассматриваемую цифровую систему можно исследовать как амплитудно-импульсную. Для этого систему с ЦВУ заменяют эквивалентной импульсной системой. На алгоритмической схеме эквивалентной системы (рис. 5.1, б) АЦП условно представляют в виде идеального импульсного элемента, а сигналы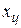 
и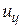 
, которые в действительности являются последовательностями чисел, заменяют соответствующими решетчатыми функциями x * и u *. Квантование по уровню при этом не учитывается (так как шаг квантования обычно достаточно мал).
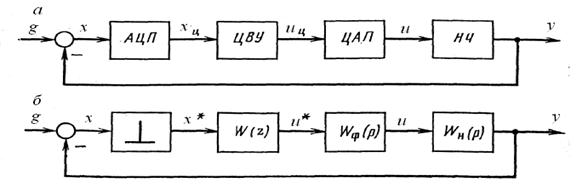
Рис. 5.1 Функциональная (а) и алгоритмическая (б) структуры цифровой системы управления
Период повторения Т условного импульсного элемента определяется периодичностью опроса датчиков Д отдельных контуров, т. е. с темпом ввода сигналов в УВМ и вывода сигналов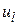 
из УВМ, который задается от специального таймера через входной и выходной коммутаторы (мультиплексор и демультиплексор). Время, затрачиваемое ЦВУ на вычисления, обычно мало по сравнению с периодом Т, и его можно не учитывать.
|
|
|
Реализуемый в ЦВУ алгоритм преобразования входной последовательности чисел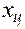 
в выходную 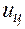на эквивалентной схеме представляют в виде соответствующей д.п.ф. 
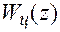, которая связывает между собой дискретные значения сигналов x * и u *. Звено с передаточной функцией 
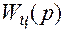называют дискретным фильтром или цифровым регулятором.
Преобразователю ЦАП в эквивалентной системе соответствует фиксирующий элемент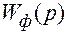 
, который в течение одного такта сохраняет мгновенное значение u *.
Д.п.ф. цифровой системы (см. рис. 5.1, а), представленной в виде эквивалентной импульсной системы (см. рис. 5.1, б),
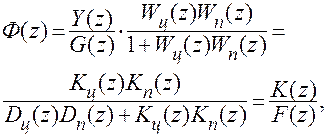(5.1)
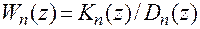— д.п.ф. приведенной непрерывной части, включающей объект, исполнительное устройство и фиксирующий элемент; 
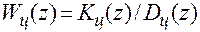— д.п.ф. цифрового регулятора.
Благодаря большим вычислительным возможностям ЭВМ в цифровых системах можно реализовать сложные алгоритмы управления и обеспечить такие переходные процессы, которые недостижимы в непрерывных системах.
Рассмотрим один из возможных подходов к решению задачи синтеза оптимальной цифровой системы. Пусть необходимо получить переходный процесс конечной длительности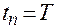 
. При этом правомерно потребовать, чтобы длительность соответствовала порядку уравнения неизменяемой части системы, который определяется главным образом объектом. Данное требование можно записать так:
,
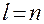где n — порядок полинома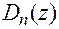 
приведенной части. С учетом условия конечной длительности найдем д.п.ф. в следующем виде:
.
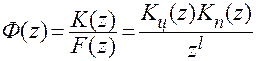Полином числителя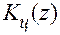 
д.п.ф. цифрового регулятора в данной задаче можно произвольно принять равным
,
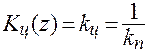где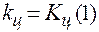 
, 
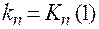— передаточные коэффициенты регулятора и приведенной части.
Так как д.п.ф.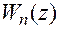 
приведенной части считается известной, то можно определить д.п.ф. ЦЗУ:
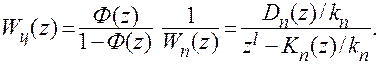(5.2)
В общем случае д.п.ф. (5.2) представляет собой отношение полиномов
.
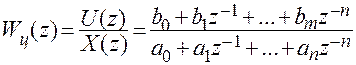Соответственно уравнение ЦВУ в операционной форме:
.
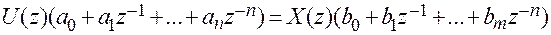Выполняя теперь обратное z -преобразование и учитывая теорему запаздывания, можно получить рекуррентную формулу
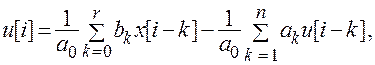(5.3)
которая связывает текущее значение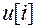 
дискретного управляющего воздействия с текущим и с предыдущими значениями сигнала ошибки, а также с предыдущими значениями управляющего воздействия.
Рекуррентная формула (5.3) легко может быть запрограммирована на ЦВМ. Для реализации программы требуется выполнение операций умножения, сложения и переадресации.
Изложенный метод позволяет синтезировать импульсную систему, оптимальную по быстродействию. Оптимальный переходный процесс достигается за счет выбора амплитуд управляющего воздействия на интервалах заданной продолжительности. В релейных системах, оптимальных по быстродействию, наименьшая длительность процесса достигается выбором моментов изменения знака постоянного по амплитуде управляющего воздействия.
Пример. Непрерывная часть цифровой системы (см. рис. 5.1 б) состоит из фиксатора и двух последовательно соединенных идеальных интегрирующих звеньев:
.
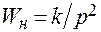Требуется определить алгоритм управления, обеспечивающий минимальную длительность переходного процесса при заданных Т =10 с и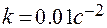 
Д.п.ф. приведенной непрерывной части системы.
.
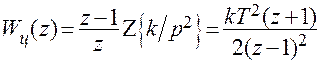Очевидно, что в данном случае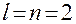 
, 
.
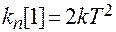Оптимальная д.п.ф. цифрового регулятора согласно формуле (5.2)
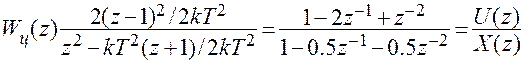
Отсюда рекуррентный алгоритм уравнения
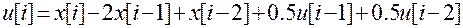
Он обеспечивает окончание переходного процесса за два периода повторения.
