Краткие конспекты лекций
Лекция 1
Многие характеристики движения сплошной среды имеют тензорную природу, поэтому рассмотрим основы тензорного исчисления и анализа в пределах, необходимых для изучения данного курса.
Система координат устанавливает соответствие между числами и точками пространства. В каждой точке трехмерного евклидового пространства есть три координатные линии, в частности, инерционной системы наблюдателя 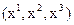 и сопутствующей системы координат
и сопутствующей системы координат 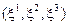 .
.
Пусть в трехмерном евклидовом пространстве задана тройка линейно- независимых векторов
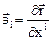 , (1.1)
, (1.1)
которые называют основными векторами базиса. Здесь 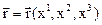 - радиус- вектор точки М пространства. Если система координат декартовая, то
- радиус- вектор точки М пространства. Если система координат декартовая, то 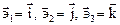 . Базисом, сопряженным по отношению к
. Базисом, сопряженным по отношению к 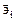 , называется тройка векторов
, называется тройка векторов 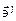 , удовлетворяющих требованиям
, удовлетворяющих требованиям 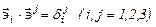 , где
, где 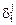 - символ Кронекера, равный единице при i=j и нулю при i¹j. Легко заметить, что
- символ Кронекера, равный единице при i=j и нулю при i¹j. Легко заметить, что 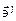 просто выражаются через
просто выражаются через 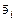 , а именно
, а именно
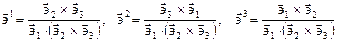 . (1.2)
. (1.2)
Вектор 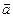 можно рассматривать как элемент векторного пространства, представленный в виде разложения по векторам основного или сопряженного базиса
можно рассматривать как элемент векторного пространства, представленный в виде разложения по векторам основного или сопряженного базиса
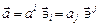 . (1.3)
. (1.3)
Из линейного разложения (1.3) легко усмотреть, что 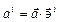 и
и 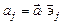 . Таким образом, равенство (1.3) можно записать в виде
. Таким образом, равенство (1.3) можно записать в виде
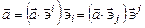 . (1.4)
. (1.4)
Заметим, что компоненты 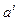 называются контровариантными, а компоненты
называются контровариантными, а компоненты 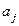 - ковариантными.
- ковариантными.
Применим (1.4) к базисным векторам 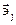 , это приводит к формулам
, это приводит к формулам
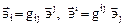 ,
,
где 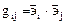 и
и 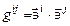 называются компонентами метрического тензора, который является симметричным,
называются компонентами метрического тензора, который является симметричным, 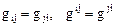 и
и 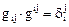 .
.
Если метрический тензор известен, то расстояние между точками 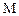 и
и 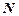 и углы между векторами
и углы между векторами 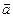 и
и 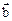 будут
будут
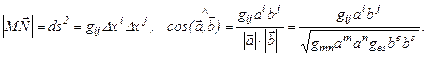
В таком случае говорят, что определена метрика данного пространства.
Пусть каждой паре векторов 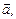
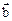 исходного трехмерного пространства, которые можно задать с помощью компонент, например, контравариантных
исходного трехмерного пространства, которые можно задать с помощью компонент, например, контравариантных 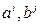 соответствует единственным образом некоторый элемент
соответствует единственным образом некоторый элемент 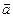
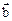 (9-мерного пространства), т.е.
(9-мерного пространства), т.е.
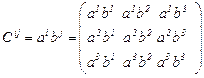 , (1.5)
, (1.5)
называемый тензорным произведением векторов 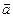 и
и 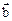 .
.
По числу и расположению свободных индексов можно судить о тензорном характере величины, выраженной в индексных обозначениях. Так, символ, который не имеет связанного с ним индекса, изображает скаляр, или, тензор нулевого ранга (например, плотность r, давление p, температура 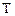 ). Тензоры первого ранга (векторы скорости
). Тензоры первого ранга (векторы скорости 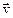 и ускорения
и ускорения 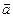 ) обозначаются основными буквами с одним свободным индексом, например,
) обозначаются основными буквами с одним свободным индексом, например, 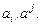 Тензоры второго ранга обозначаются символами с двумя свободными индексами, например, тензоры деформаций
Тензоры второго ранга обозначаются символами с двумя свободными индексами, например, тензоры деформаций 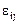 , скоростей деформаций
, скоростей деформаций 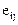 и напряжений
и напряжений 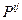 .
.
Следует отметить, что все операции над тензорами инвариантны, т.е. не зависят от преобразований системы координат. Причем имеют место только такие операции, после которых получается опять тензор.
а) Перестановка индексов.
Если в рассматриваемом тензоре 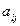 провести перестановку индексов и получить новый объект
провести перестановку индексов и получить новый объект 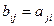 , то последний определяет также тензор, в силу того, что перестановка является инвариантной
, то последний определяет также тензор, в силу того, что перестановка является инвариантной
б) Сложение (вычитание) тензоров.
Складывать можно тензора одной и той же валентности. Например, если 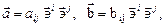 то
то 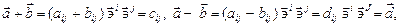
т.е. сумма (вычитание) двух тензоров есть тензор той же валентности.
в) Умножение тензора на число, например, 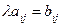 .
.
г) Симметрирование и альтернирование.
Если имеется тензор второго ранга 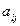 , то операция, дающая также тензор второго ранга
, то операция, дающая также тензор второго ранга 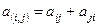 называется симметрированием, т.е.
называется симметрированием, т.е. 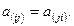
В результате операции 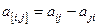 получается тензор второго ранга
получается тензор второго ранга 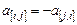 . Такая операция носит название – альтернированием, а тензор – антисимметричным тензором.
. Такая операция носит название – альтернированием, а тензор – антисимметричным тензором.
Следовательно, всегда имеет место соотношение вида
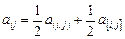 .
.
д) Поднятие и опускание индексов.
Эта операция производится с помощью метрического тензора. Так, для операции опускания индексов имеем 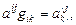
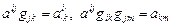 .
.
При поднятии индексов получаем, например, 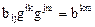 .
.
Введем понятие градиента тензора с помощью символического вектора (оператора) Гамильтона 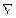 (набла), который равен
(набла), который равен
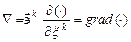 .
.
Например, градиент тензора нулевого ранга (температуры) есть 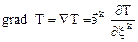 .
.
Итак, градиент тензора есть тензор валентности на единицу большей, чем валентность исходного тензора.
Дивергенцией тензора называется скалярное произведение символического вектора 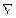 (набла) на этот тензор. Например, дивергенция вектора
(набла) на этот тензор. Например, дивергенция вектора 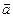 есть скаляр.
есть скаляр.
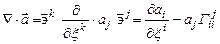 .
.
В случае декартовой системы координат
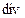
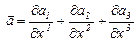 .
.
Ротором тензора называется векторное произведение символического вектора 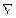 на этот тензор, а именно, псевдотензор. Например, в случае декартовой системы координат ротор вектора
на этот тензор, а именно, псевдотензор. Например, в случае декартовой системы координат ротор вектора 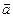 есть псевдовектор
есть псевдовектор
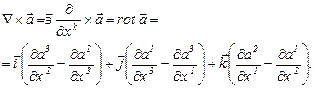
Оператором Лапласа (лапласианом) называется дифференциальный оператор 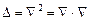 . Например, оператор от температуры
. Например, оператор от температуры 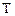 (тензор нулевого ранга) есть лапласиан вида
(тензор нулевого ранга) есть лапласиан вида 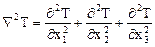 .
.
 2021-12-25
2021-12-25 274
274







