2021-12-25
325
Лекция 5
Выражение тензора деформаций через компоненты вектора перемещения
Рассмотрим случай, когда начальное состояние может реально осуществляться и его метрика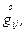 
как и метрика 
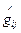является евклидовой. В этом случае можно ввести вектор перемещения 
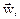а именно 
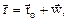где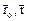 
- радиусы – векторы относительно системы отсчета 
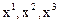одной и той же точки M сплошной среды в начальный момент времени 
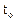и в данный момент 
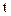соответственно.
Нетрудно получить
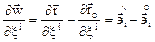
откуда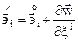 
или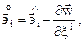 
поэтому
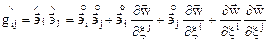
и
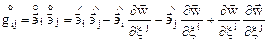
Следовательно,
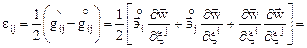
(5.1)
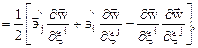
где первые производные от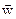 
по координатам 
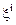характеризуют относительные перемещения точек сплошной среды.
Вектор перемещения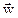 
можно разложить как в актуальном пространстве, 
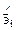, так и в начальном 
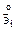и соответственно этому ввести два сорта компонент одного и того же вектора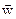
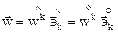
можно ввести и два сорта ковариантных производных
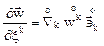и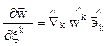 
. (5.2)
Подставим первое из (5.2) в (5.1), получим
.
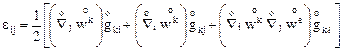Так как компоненты метрического тензора можно, не меняя результата, вводить под знак ковариантной производной, имеем
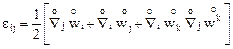. (5.3)
Аналогично, с помощью второго равенства из (5.2) и (5.1) получим
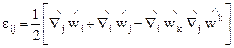. (5.3)
В случае бесконечно малых относительных перемещений после отбрасывания квадратичных по 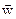членов получим
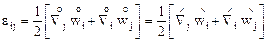. (5.4)
В декартовой системе координат
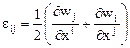. (5.5)
Лекция 6
