С другой точкой зрения, называемой именем Эйлера, объектом изучения является не сама среда, а неподвижное пространство, заполненное движущейся средой. Изучаются изменения различных тензорных характеристик среды в фиксированной точке 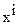 пространства с течением времени и изменения этих характеристик при переходе в фиксированный момент времени к другим точкам пространства. Иначе говоря, различные характеристики движения, рассматриваются как функции координат
пространства с течением времени и изменения этих характеристик при переходе в фиксированный момент времени к другим точкам пространства. Иначе говоря, различные характеристики движения, рассматриваются как функции координат 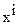 точки и времени t. Переменные
точки и времени t. Переменные 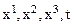 называются переменными Эйлера.
называются переменными Эйлера.
Поле вектора перемещений. Компоненты вектора перемещений в переменных Эйлера определяются формулами
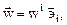
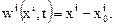
Поле перемещений называют стационарным, если вектор перемещения в каждой точке не зависит от времени, т.е. 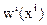 и нестационарным в общем случае когда
и нестационарным в общем случае когда 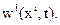
Поле вектора скорости. Рассмотрим поле скоростей 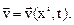 Значения компонент скорости в переменных Эйлера получим из формул (3.1).
Значения компонент скорости в переменных Эйлера получим из формул (3.1).
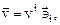
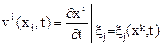 .
.
Поле скоростей называют стационарным, а движение среды установившимся, если вектор скорости не зависит от t в каждой точке поля
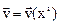 или
или 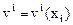 .
.
В общем случае, когда скорость зависит и от координат и от времени 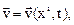 скоростное поле называют нестационарным, а движение среды – неустановившимся.
скоростное поле называют нестационарным, а движение среды – неустановившимся.
Поле вектора ускорения. Ускорение частицы 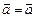
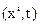 определяется как индивидуальная производная по времени от вектора скорости
определяется как индивидуальная производная по времени от вектора скорости
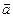
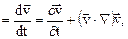
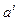
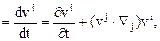
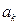
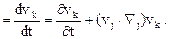
Локальная производная 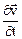 называется локальным ускорением и оно характеризует изменение скорости в каждой точке пространства (неподвижного). Конвективная производная называется конвективным ускорением и оно характеризует изменение скорости при переходе от одной точки пространства к соседним точкам.
называется локальным ускорением и оно характеризует изменение скорости в каждой точке пространства (неподвижного). Конвективная производная называется конвективным ускорением и оно характеризует изменение скорости при переходе от одной точки пространства к соседним точкам.
Взаимосвязь методов Лагранжа и Эйлера
Пусть известно движение среды в переменных Лагранжа. Это значит, что установлены значения перемещений, скоростей, температуры, уравнение движения и т.д. как функции переменных Лагранжа:
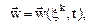
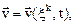
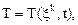
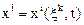 и т.д.
и т.д.
Чтобы перейти к переменным Эйлера, разрешим уравнения движения относительно переменных 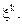 Это можно сделать, ибо
Это можно сделать, ибо 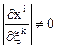 во время движения.
во время движения.
Тогда имеем
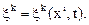
Подставив значения лагранжевых координат в формулы найдем перемещение, скорость, температуру и т.д., как функции переменных Эйлера:
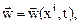
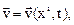
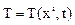 и т.д.
и т.д.
Наоборот, пусть движение среды задано в переменных Эйлера. т.е. известны все характеристики среды, в том числе и скорость, как функции переменных 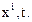
На уравнение, определяющее компоненты скорости
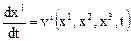 ,
, 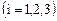
можно смотреть как на систему трех линейных дифференциальных уравнений относительно функций 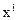 . Проинтегрировав эту систему, найдем величину
. Проинтегрировав эту систему, найдем величину 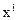 как функции t и трех постоянных
как функции t и трех постоянных 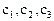
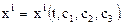
Значения постоянных определяются из начальных условий (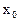 при
при 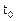 ) и, следовательно, эти постоянные являются параметрами, индивидуализирующими точку сплошной среды – переменными Лагранжа.
) и, следовательно, эти постоянные являются параметрами, индивидуализирующими точку сплошной среды – переменными Лагранжа.
Линии, касательные к которым в каждой точке пространства будут совпадать в данный момент 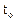 с направлением вектора скорости
с направлением вектора скорости 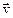 в этой точке, называются линиями тока.
в этой точке, называются линиями тока.
Запишем условие того, что элемент
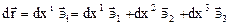 ,
,
взятый вдоль линии тока и вектор скорости
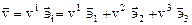
параллельны друг другу, т.е.
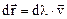 ,
,
где 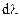 - скалярный параметр. В компонентах получаем
- скалярный параметр. В компонентах получаем
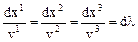
или
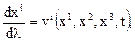
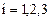 . (3.5)
. (3.5)
Это и есть дифференциальные уравнения линий тока. Они отличаются от дифференциальных уравнений траектории движения частиц среды, которые, как известно, имеют вид
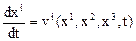 . (3.6)
. (3.6)
Причем, при интегрировании (3.5) t следует рассматривать как постоянный параметр, а в уравнениях (3.6) t необходимо считать переменным.
Таким образом, линии тока, вообще говоря, не совпадают с траекториями. Семейство линии тока 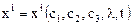 зависит от времени и в разные моменты времени разное. Однако параметр
зависит от времени и в разные моменты времени разное. Однако параметр 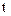 входит в правые части (3.5) и (3.6) только в случае неустановившихся движений. В случае установившихся движений разница между уравнениями (3.5) и (3.6) пропадает, она сводится только к разному обозначению параметра по которому проводится дифференцирование, что не играет никакой роли.
входит в правые части (3.5) и (3.6) только в случае неустановившихся движений. В случае установившихся движений разница между уравнениями (3.5) и (3.6) пропадает, она сводится только к разному обозначению параметра по которому проводится дифференцирование, что не играет никакой роли.
Поэтому в случае стационарного движения линии тока и траектории совпадают.
Как для всякого векторного поля, для поля вектора вихря скорости 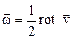 можно ввести понятие вихревых линий и трубок. Вихревой линией называется линия, касательная к каждой точке которой совпадает с направлением вектора вихря
можно ввести понятие вихревых линий и трубок. Вихревой линией называется линия, касательная к каждой точке которой совпадает с направлением вектора вихря 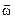 . Дифференциальное уравнение вихревых линий имеет вид
. Дифференциальное уравнение вихревых линий имеет вид
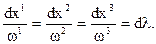 (3.7)
(3.7)
 2021-12-25
2021-12-25 299
299








