Лекция 4
Рассмотрим два произвольных положения деформируемого тела и, в частности, его частиц 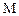 и
и 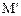 в произвольные моменты времени t и
в произвольные моменты времени t и 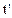
Векторы базиса в точке 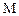 в момент
в момент 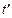 обозначим через
обозначим через 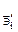 , а в момент t- через
, а в момент t- через 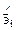 . Очевидно, в сопутствующей системе координат будем иметь
. Очевидно, в сопутствующей системе координат будем иметь
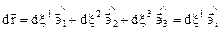 ,
,
и
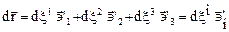 .
.
Пусть в момент t
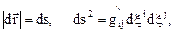
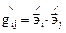 (4.1)
(4.1)
и в момент 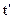
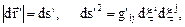
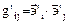 . (4.2)
. (4.2)
Подчеркнем, что координаты точек 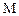 и
и 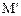 в моменты t и
в моменты t и 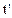 в соответствующей системе координат одинаковые, а компоненты метрических тензоров
в соответствующей системе координат одинаковые, а компоненты метрических тензоров 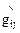 и
и 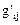 разные.
разные.
Введем в рассмотрение так называемый коэффициент относительного удлинения через отношение
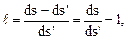 (4.3)
(4.3)
Деформацию среды в окрестности каждой частицы можно полностью описать с помощью тензора второго ранга.
Введем такой тензор
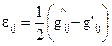 . (4.4)
. (4.4)
Так как деформация среды связана с изменением расстояний, между частицами, то за меру деформации можно принять разность
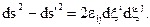 (4.5)
(4.5)
В левой части равенства (4.5) стоит величина 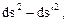 а в правой части – произведение некоторого объекта второго ранга
а в правой части – произведение некоторого объекта второго ранга 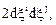 на произвольной тензор второго ранга
на произвольной тензор второго ранга 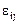 который называется тензором деформаций.
который называется тензором деформаций.
Геометрический смысл компонент тензора деформаций
Выясним теперь геометрический смысл ковариантных компонент тензора деформаций. Запишем компоненты метрических тензоров в следующем виде:
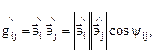 (4.6)
(4.6)
где 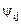 углы между векторами
углы между векторами 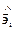 и
и 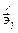 и
и
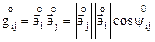 , (4.7)
, (4.7)
где 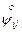 углы между векторами
углы между векторами 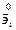 и
и 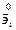 . Составим соотношение
. Составим соотношение
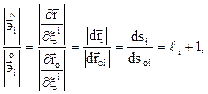
где 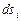 и
и 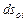 – элементы дуг координатных линий
– элементы дуг координатных линий 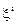 , а
, а 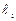 - коэффициенты относительных удлинении в направлениях
- коэффициенты относительных удлинении в направлениях 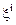 . Тогда
. Тогда
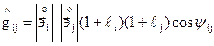 ,
,
а приняв за состояние сплошной среды в момент 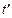 начальное состояние или «начальное состояние»
начальное состояние или «начальное состояние» 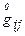 , получим следующие формулы
, получим следующие формулы
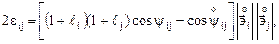 (4.8)
(4.8)
которые удобны для геометрического истолкования 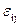 .
.
Рассмотрим сначала геометрическое истолкование 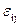 с одинаковыми индексами. Из (4.8) будем иметь
с одинаковыми индексами. Из (4.8) будем иметь
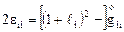 ,
,
откуда
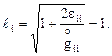 (4.9)
(4.9)
Если деформации малы, то 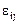 малы и разложив (4.9) в ряд, получим
малы и разложив (4.9) в ряд, получим
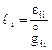 .
.
Кроме того, если сопутствующая система в «начальном состоянии» взята декартовой, но 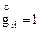 , и поэтому
, и поэтому
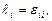 (4.10)
(4.10)
т.е ковариантные компоненты тензоров деформаций с одинаковыми индексами в случае бесконечно малых деформаций совпадают с коэффициентами относительных удлинений вдоль декартовых осей координат начального состояния.
Обратимся к вопросу о геометрическом истолковании компонент 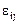 с различными индексами (i¹j). Для простоты в «начальном состоянии» выберем в данной точке такую систему координат, в которой
с различными индексами (i¹j). Для простоты в «начальном состоянии» выберем в данной точке такую систему координат, в которой 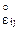 взаимно ортогональны, т.е.
взаимно ортогональны, т.е.
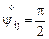 .
.
Тогда положив
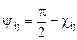
из (4.9), (4.7) и (4.4) получим
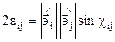
или
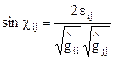 , (4.11)
, (4.11)
откуда видно, что в общем случае углы, бывшие в «начальном состоянии» прямыми, после деформации перестают быть прямыми и ковариантные компоненты 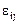 с различными индексами (i¹j) характеризуют скашивание первоначально прямого координатного угла. Если деформации бесконечно малы и система координат в «начальном состоянии» декартова, то
с различными индексами (i¹j) характеризуют скашивание первоначально прямого координатного угла. Если деформации бесконечно малы и система координат в «начальном состоянии» декартова, то 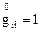 ,
, 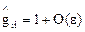 , где e - бесконечно малая величина. С помощью разложения в ряд получим
, где e - бесконечно малая величина. С помощью разложения в ряд получим
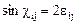
или ввиду малости деформации
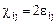 (3.12)
(3.12)
 2021-12-25
2021-12-25 619
619








