2021-12-25
156
Лекция 7
Тензор деформаций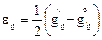 
вводится в связи с двумя состояниями сплошной среды, данным 
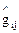и, вообще говоря, «начальным».
Помимо этих двух состояний сплошной среды рассмотрим еще состояние в момент времени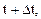 
близкий к рассматриваемому данному состоянию 
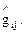Компоненты метрического тензора в этот момент 
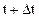обозначим через 
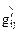. Очевидно, можно ввести компоненты тензора деформаций по отношению к состояниям сплошной среды в моменты 
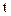и 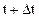. Обозначим эти компоненты через 
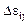и запишем
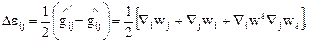(7.1)
Формула (7.1) имеет место, так как перемещение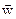 
из состояния в момент 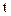в состояние в момент 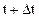существует.
Очевидно, что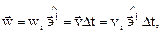 
где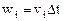 
имеет порядок 
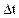и является бесконечно малым перемещением, если 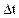мало.
Поэтому
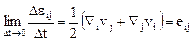
Величины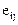 
являются компонентами симметричного тензора, который называется тензором скоростей деформаций.
Если поле скоростей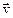 
известно, то компоненты 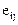можно вычислить по формуле
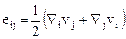. (7.2)
Выразим скорость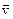 
любой частицы (М) через скорость 
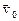движения частицы ей смежной (
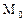). Для этого разложим скорость 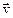в окрестности точки М в ряд Тейлора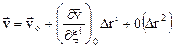 
или
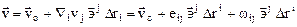. (7.3)
В последней формуле 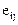и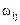 
- соответственно, симметричный и антисимметричный тензоры, имеют вид
.
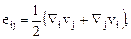
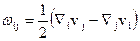Рассмотрим механическое истолкование каждого члена формулы (7.3).
Если тензор скоростей деформаций 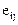=0, то
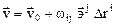(7.4)
и движение в окрестности точки 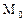будет вращением абсолютного твердого тела. В случае 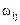=0 формула (7.4) определяет поступательное движение а.т.т. со скоростью 
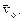По этой причине поле скоростей называют безвихревым («безвращательным»), если тензор 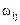- тензор завихренности – обращается в нуль во всех точках.
Компоненты тензора скоростей деформаций имеют следующий физический смысл. Диагональные компоненты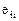 
определяют скорости относительного удлинения отрезков сплошной среды, а недиагональные компоненты 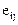характеризуют скорости скошения, например, первоначально прямых углов.
