Результаты предыдущих рассуждений приводят к теореме Коши-Гельмгольца о разложении скорости точек бесконечно малой частицы сплошной среды: «Любое движение элементарного объема сплошной среды можно в данное мгновение рассматривать как результат сложения двух движений: квазитвердого, состоящего из поступательного и вращательного движений, и деформационного», а именно
.
Лекция 8
Массу можно ввести как для всего объема 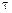 , так и для любой его частицы, т.е.
, так и для любой его частицы, т.е. 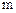 и
и 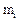 . Тогда
. Тогда
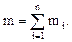
В МСС вместо массы вводится понятие плотности среды 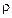 , которая определяется следующим образом. Отношение
, которая определяется следующим образом. Отношение
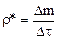 есть среднее распределение массы или средняя плотность вещества в объеме
есть среднее распределение массы или средняя плотность вещества в объеме 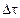 . Истинная плотность среды в данной точке определяется как следующий предел
. Истинная плотность среды в данной точке определяется как следующий предел
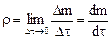 .
.
Плотность среды 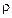 является скалярной функцией переменных Лагранжа и Эйлера, т.е.
является скалярной функцией переменных Лагранжа и Эйлера, т.е.
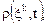
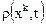 .
.
Очевидно, при заданной плотности 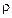 среды масса элементарного объема этой среды определяется как
среды масса элементарного объема этой среды определяется как 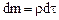 , а масса всего тела объема
, а масса всего тела объема 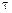
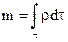 .
.
Так как изменение со временем всякой величины характеризуется индивидуальной производной по времени, то закон сохранения массы математически записывается в виде
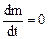 или
или 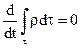 . (8.1)
. (8.1)
Пусть 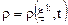 , тогда принцип сохранения массы (4.1) при учете, что
, тогда принцип сохранения массы (4.1) при учете, что 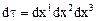 и
и 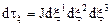 , где
, где 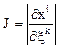 - якобиан преобразований координат, запишется в виде
- якобиан преобразований координат, запишется в виде 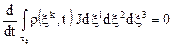 .
.
Действительно, внося производную по времени под знак интеграла, получим
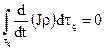 .
.
Откуда, в силу произвольности выбора объема имеем
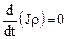 . (8.2)
. (8.2)
Это дифференциальное уравнение и является уравнением неразрывности в дифференциальной форме в переменных Лагранжа.
Найдем теперь вид уравнения неразрывности в эйлеровых переменных. Если воспользоваться в (8.1) правилом дифференцирования, установленного в тензорном анализе интеграла, взятого по подвижному объему, при соблюдении закона сохранения массы, будем иметь
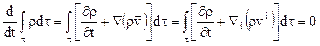 .
.
В силу произвольности выбора объема, получаем основное дифференциальное уравнение МСС
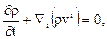 (8.3)
(8.3)
которое носит название уравнения неразрывности в переменных Эйлера. Используя правило векторного анализа и определение индивидуальной производной, можно переписать (4.3) в виде
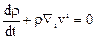 .
.
В частном случае, когда поле плотности стационарно, уравнение неразрывности (8.3) принимает форму
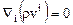 .
.
Последнее в прямоугольной декартовой системе координат имеет вид
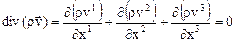 .
.
Если среда является несжимаемой, уравнение неразрывности дает
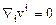 .
.
В декартовых прямоугольных координатах имеем соотношение
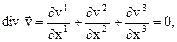
 2021-12-25
2021-12-25 47
47








