Лекция 9
Силы, распределенные по объему 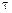 или по всей массе, называются объемными или массовыми силами.
или по всей массе, называются объемными или массовыми силами.
Обозначим через 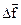 главный вектор массовых сил, действующих на элемент массы
главный вектор массовых сил, действующих на элемент массы 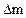 . Тогда вектор плотности распределения массовой силы в данной точке есть
. Тогда вектор плотности распределения массовой силы в данной точке есть
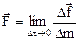 .
.
Предполагается, что вектор плотности силы 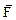 зависит от выбранной точки
зависит от выбранной точки 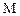 и времени, т.е.
и времени, т.е.
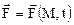 .
.
Эффект действия массовых сил на деформируемую сплошную среду объема 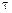 выражается через главный вектор и главный момент
выражается через главный вектор и главный момент
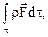
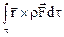 .
.
В МСС основную роль играют не массовые, а поверхностные силы. Поверхностными силами называются силы, распределенные по поверхности 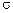 сплошной среды.
сплошной среды.
Обозначим через 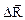 главный вектор поверхностных сил, действующих на элементарную площадку
главный вектор поверхностных сил, действующих на элементарную площадку 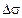 . Тогда соотношение
. Тогда соотношение
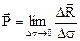
определяет вектор плотности распределения поверхностных сил, действующих на площадку 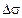 .
.
Примерами могут служить силы вязкого взаимодействия двух касающихся объемов 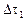 и
и 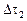 , силы давления, архимедова сила и др. Вектор
, силы давления, архимедова сила и др. Вектор 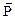 называют также вектором напряжений на данной площадке
называют также вектором напряжений на данной площадке 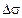 .
.
Относительно вектора плотности поверхностных сил 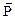 принимается, что он зависит только от времени, от взятой точки
принимается, что он зависит только от времени, от взятой точки 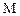 и от направления нормали
и от направления нормали 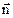 к поверхности в этой точке, но не зависит от вида самой поверхности, т.е.
к поверхности в этой точке, но не зависит от вида самой поверхности, т.е.
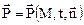 .
.
Эффект действия поверхностных сил на все тело характеризуется главным вектором и главным моментом: 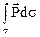 ,
, 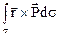 .
.
Докажем, что вектор напряжений можно представить как произведение орта 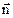 на тензор второго ранга, который является функцией только координат и времени.
на тензор второго ранга, который является функцией только координат и времени.
Для этого рассмотрим вырезанный в среде элементарный тетраэдр с вершиной в точке.
Обозначим площадь треугольника АВС через 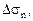 а площади треугольников ВМС, АМС и АМВ соответственно
а площади треугольников ВМС, АМС и АМВ соответственно 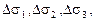 причем индексы 1,2,3 при этих площадках, так
причем индексы 1,2,3 при этих площадках, так
же как и при напряжениях 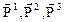 приложенных к этим площадкам, означают ось координат, перпендикулярную к данной площадке
приложенных к этим площадкам, означают ось координат, перпендикулярную к данной площадке 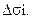
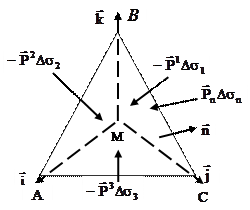
Рассматривая взятый бесконечно малый тетраэдр как абсолютно твердое тело, напишем уравнение движения центра инерции этой системы, общая масса которой пусть равна 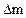 , а именно
, а именно
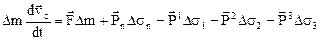 , (9.1)
, (9.1)
где 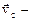 вектор скорости центра инерции тетраэдра,
вектор скорости центра инерции тетраэдра, 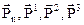 - векторы напряжений, приложенные к соответствующим площадкам.
- векторы напряжений, приложенные к соответствующим площадкам.
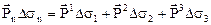 .
.
Замечая, что 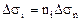 , получим
, получим
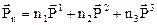 или
или 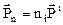 . (9.2)
. (9.2)
В проекциях на оси координат имеем
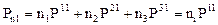 ,
,
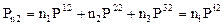 , (9.3)
, (9.3)
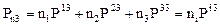 .
.
Зависимость вектора напряжений 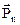 от векторов напряжений
от векторов напряжений 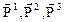 на координатных площадках может быть с помощью (9.3) записана в виде
на координатных площадках может быть с помощью (9.3) записана в виде
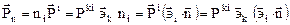 . (9.4)
. (9.4)
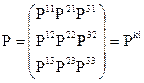 . (9.5)
. (9.5)
Этот тензор называется тензором внутренних напряжений или просто тензором напряжений.
 2021-12-25
2021-12-25 155
155








