Лекция 15
Сплошная среда по определению называется упругой средою, если состояние деформации характеризуется тензором деформации 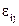 ; в среде можно выделить некоторое состояние, называемое естественным, в котором отсутствуют как напряжения, так и деформации, т.е.
; в среде можно выделить некоторое состояние, называемое естественным, в котором отсутствуют как напряжения, так и деформации, т.е. 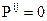 при
при 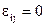 ; для всех состояний этой среды в любой точке и в любой момент времени тензор напряжений
; для всех состояний этой среды в любой точке и в любой момент времени тензор напряжений 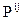 является взаимно- однозначной функцией тензора деформаций
является взаимно- однозначной функцией тензора деформаций 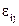 . Из этого вытекает, что в общем случае закон поведения упругой сплошной среды имеет вид
. Из этого вытекает, что в общем случае закон поведения упругой сплошной среды имеет вид
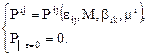 (15.1)
(15.1)
Теория упругости называется линейной физически, если напряжения линейно зависят от деформаций. Частным случаем линейной теории упругости является классическая теория упругости. Линейное упругое тело называется классическим, если оно дополнительно удовлетворяет гипотезам однородности и изотропности.
Чтобы выполнялось требование линейности относительно тензора деформаций, должно быть
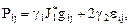
где 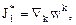 a величины
a величины 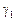 и
и 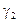 , вообще говоря, могут быть функциями термодинамических параметров
, вообще говоря, могут быть функциями термодинамических параметров 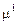 . В случае когда
. В случае когда 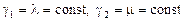 , закон поведения (15.2) называют законом Гука для изотропной упругой среды (линейное упругое тело Гука), а параметры l и m - упругими постоянными Ламе.
, закон поведения (15.2) называют законом Гука для изотропной упругой среды (линейное упругое тело Гука), а параметры l и m - упругими постоянными Ламе.
Обратимся к построению замкнутой системы уравнений, определяющей модель упругого тела Гука.
Для линейного упругого тела уравнение неразрывности имеет вид
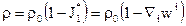 , (15.3)
, (15.3)
где полагается, что тело в естественном состоянии является однородным 
В силу малости перемещений и скоростей можно принять
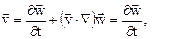
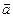
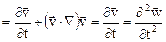 .
.
Тогда уравнение динамики через перемещения примет вид
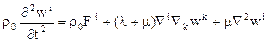 . (15.4)
. (15.4)
Соотношения (15.3) и (15.4) образуют систему уравнений для определения перемещений и плотности. Величины 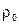 и
и 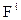 считаются заданными. Уравнения (15.4) называются уравнениями Ламе. Уравнения Ламе выведены в предположении, что деформации малы. Уравнение неразрывности (15.3) в линейной теории упругости с малыми деформациями можно не рассматривать. Поэтому в уравнениях (15.4) с точностью до малых первого порядка можно писать
считаются заданными. Уравнения (15.4) называются уравнениями Ламе. Уравнения Ламе выведены в предположении, что деформации малы. Уравнение неразрывности (15.3) в линейной теории упругости с малыми деформациями можно не рассматривать. Поэтому в уравнениях (15.4) с точностью до малых первого порядка можно писать 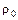 вместо
вместо 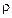 .
.
 2021-12-25
2021-12-25 450
450







