Уравнения динамики сплошной среды. Уравнение момента количества движения.
Основным динамическим уравнением движения материальной точки является второй закон Ньютона
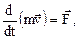
утверждающий, что индивидуальная производная по времени от количества движения материальной точки равняется силе, приложенной в этой точке.
Обобщение уравнения движения материальной точки на систему 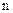 дискретных точек является уравнение количества движения системы материальных точек
дискретных точек является уравнение количества движения системы материальных точек
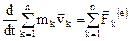 .
.
Обобщим теперь это уравнение на случай движения сплошной среды объема 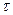 с поверхностью
с поверхностью 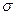 под действием массовых и поверхностных сил. Это уравнение записывается в виде
под действием массовых и поверхностных сил. Это уравнение записывается в виде
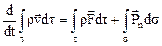 . (10.1)
. (10.1)
Таким образом, индивидуальная производная по времени от количества движения объема 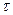 сплошной среды равна сумме всех внешних действующих на него массовых и поверхностных сил.
сплошной среды равна сумме всех внешних действующих на него массовых и поверхностных сил.
В частности, для случая непрерывных движений интегральная форма уравнения движения (4.9) может быть заменена дифференциальным соотношением.
Преобразуем поверхностный интеграл (10.1) в объемный по формуле Гаусса- Остроградского
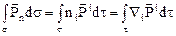 .
.
Тогда из уравнения количества движения получим
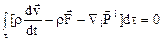 .
.
Отсюда, ввиду произвольности объема, получаем следующее дифференциальное уравнение
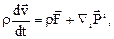 (10.2)
(10.2)
которое называют основным уравнением динамики сплошной среды в «напряжениях». Векторное равенство (10.2) эквивалентно в системе координат 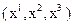 следующим трем скалярным равенствам
следующим трем скалярным равенствам
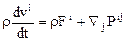 , (10.3)
, (10.3)
Если среда покоится, то скорость и перемещение ее частиц равны нулю, т.е. 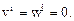
В этом случае из уравнения (10.3) следует, что при равновесии сплошной среды объемные силы уравновешиваются внутренними поверхностными силами, т.е.
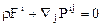 . (10.4)
. (10.4)
Уравнения (10.4) есть уравнения равновесия сплошной среды.
Обобщим теперь уравнение момента количества движения системы на среду, занимающую объем 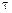 с поверхностью
с поверхностью 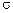
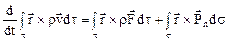 , (10.5)
, (10.5)
т.е. примем, что индивидуальная производная по времени от момента количества движения сплошной среды объема 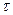 относительно некоторого центра (связанного с инерциальной системой отсчета) равна сумме моментов внешних массовых и поверхностных сил, действующих на этот объем относительно того же центра.
относительно некоторого центра (связанного с инерциальной системой отсчета) равна сумме моментов внешних массовых и поверхностных сил, действующих на этот объем относительно того же центра.
Уравнение момента количества движения (10.5) в случае непрерывного движения и на основании формулы Гаусса-Остроградского можно записать в эквивалентной форме
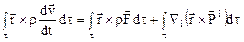 .
.
Так как, в силу того, что ковариантная производная от векторного произведения равна
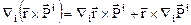 ,
,
легко видеть, что формулу можно представить в виде суммы двух следующих интегралов
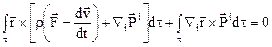 .
.
Первый из этих интегралов обращается в нуль на основании динамических уравнений движения (10.1), поэтому
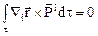 ,
,
откуда в силу произвольности объема 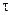 , следует что
, следует что
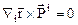 , (10.6)
, (10.6)
т.е. в классическом случае, при отсутствии внутренних моментов массовых и поверхностных распределенных пар, уравнение кинетического момента (10.5) приобретает вид (10.6).
Так как 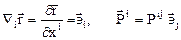 , уравнение (10.6) приобретает вид
, уравнение (10.6) приобретает вид
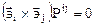 .
.
Последнее, очевидно, можно записать еще следующим образом:
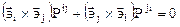
или
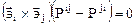 .
.
Откуда вытекает, что
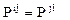 при
при 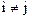 .
.
Таким образом, уравнение моментов в классическом случае сводится к следствию – тензор напряжений симметричен.
Лекция 11
 2021-12-25
2021-12-25 246
246








