Возьмем вектор 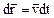 - вектор перемещения бесконечно малого объема сплошной среды
- вектор перемещения бесконечно малого объема сплошной среды 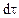 за время
за время 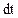 ; умножим скалярно уравнение импульсов 10.2 на
; умножим скалярно уравнение импульсов 10.2 на 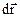 и проинтегрируем по объему
и проинтегрируем по объему 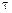 . Получим
. Получим

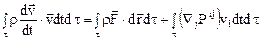 . (11.1)
. (11.1)
Преобразуем каждый из входящих в это соотношение интегралов. Так как масса 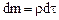 постоянна, то, очевидно, что
постоянна, то, очевидно, что
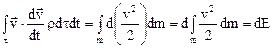 .
.
Массовые силы 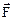 разобьем на две группы:
разобьем на две группы: 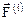 - внутренние и
- внутренние и 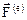 - внешние по отношению ко всему объему
- внешние по отношению ко всему объему 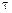 . Тогда
. Тогда
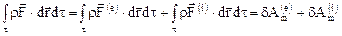 ,
,
где 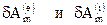 - элементарные работы внешних и внутренних массовых сил, действующих на объем с массой
- элементарные работы внешних и внутренних массовых сил, действующих на объем с массой  при бесконечно малом перемещении.
при бесконечно малом перемещении.
Заметим, что сумма всех внутренних массовых сил равна нулю, а работа этих сил может отличаться от нуля.
Последний интеграл в выражении (5.1) запишем в виде следующих двух интегралов
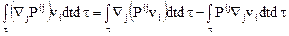 .
.
В силу очевидного тождества
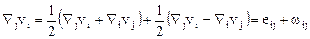
и воспользовавшись формулой Гаусса –Остроградского, получим
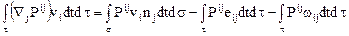 .
.
В силу антисимметрии тензора 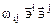 имеем
имеем
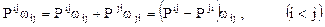 .
.
Поэтому в классическом случае 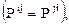 последний интеграл равен нулю.
последний интеграл равен нулю.
Так как 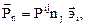
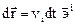 можно записать
можно записать
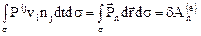 ,
,
где через 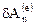 обозначена работа внешних поверхностных сил. Работой внутренних поверхностных сил напряжений в объеме назовем интеграл
обозначена работа внешних поверхностных сил. Работой внутренних поверхностных сил напряжений в объеме назовем интеграл
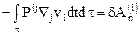 ,
,
являющийся инвариантной величиной.
Таким образом, равенство (11.1) можно записать в виде
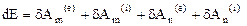 , (11.2)
, (11.2)
Лекция 12
Первый закон термодинамики. Уравнение притока тепла.
Рассмотрим систему, которая характеризуется конечным числом определяющих параметров. Будем подразумевать, что с точки зрения данных о характеристиках внутреннего состояния частицы 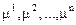 и их бесконечно малых изменений
и их бесконечно малых изменений 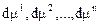 можно судить о различных суммарных макроскопических притоках энергии к частице извне. Полный внешний приток энергии для элементарного процесса
можно судить о различных суммарных макроскопических притоках энергии к частице извне. Полный внешний приток энергии для элементарного процесса 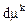 к бесконечно малому объему среды можно представить в виде суммы
к бесконечно малому объему среды можно представить в виде суммы
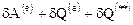 ,
,
где 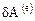 - элементарная работа внешних макроскопических массовых и поверхностных сил,
- элементарная работа внешних макроскопических массовых и поверхностных сил, 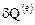 - элементарный приток тепла к телу извне, а
- элементарный приток тепла к телу извне, а 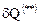 - элементарный приток энергии за счет других источников притока энергии (химической реакции, ионизации, диссипации и т.д.).
- элементарный приток энергии за счет других источников притока энергии (химической реакции, ионизации, диссипации и т.д.).
Первый закон термодинамики, или закон сохранения энергии, можно сформулировать как невозможность осуществления вечного двигателя первого рода, т.е. циклически работающей машины, которая могла бы служить источником полезной энергии, без использования какого-либо внешнего по отношению к этой машине источника энергии. Таким образом, из первого закона термодинамики следует, что существует функция состояния 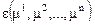 , полный дифференциал которой для осуществимых процессов равен сумме элементарных работ внешних массовых и поверхностных макроскопических сил и элементарных притоков к системе извне других видов энергии, т.е.
, полный дифференциал которой для осуществимых процессов равен сумме элементарных работ внешних массовых и поверхностных макроскопических сил и элементарных притоков к системе извне других видов энергии, т.е.
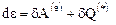 , (12.1)
, (12.1)
которое используется для определения полной энергии системы 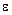 . И, наоборот, если энергия
. И, наоборот, если энергия 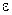 известна, то (12.1) можно использовать для выяснения механизма взаимодействия элементарного объема с внешними телами, т.е. для определения
известна, то (12.1) можно использовать для выяснения механизма взаимодействия элементарного объема с внешними телами, т.е. для определения 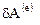 и
и 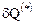 .
.
Положим
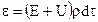 ,
,
где 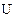 - скалярная функция параметров состояния, называемая плотностью внутренней энергии. Плотность внутренней энергии или удельная внутренняя энергия
- скалярная функция параметров состояния, называемая плотностью внутренней энергии. Плотность внутренней энергии или удельная внутренняя энергия 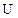 , как и полная энергия системы
, как и полная энергия системы 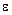 , определяется с точностью до аддитивной постоянной и существует для каждой термодинамической системы. Полная энергия произвольного объема
, определяется с точностью до аддитивной постоянной и существует для каждой термодинамической системы. Полная энергия произвольного объема 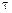 сплошной среды определяется следующим образом
сплошной среды определяется следующим образом
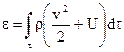 .
.
Таким образом, универсальное соотношение, выражающее собой закон сохранения энергии, можно представить в виде
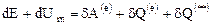 , (12.2)
, (12.2)
где 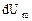 - изменение внутренней энергии рассматриваемого тела,
- изменение внутренней энергии рассматриваемого тела, 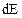 - изменение его кинетической энергии.
- изменение его кинетической энергии.
Вычитая из соотношения (12.2) равенство (11.2), выражающее теорему живых сил для сплошной среды, получим уравнение
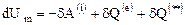 (12.3)
(12.3)
или
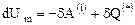 ,
,
которое носит название уравнения притока тепла и может заменить собой закон сохранения энергии.
Уравнение притока тепла (12.3) можно записать для любых мысленно выделенных объемов сплошной среды.
Составим его для бесконечно малого объема 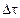 . Для плотности
. Для плотности 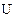 внутренней энергии имеем
внутренней энергии имеем
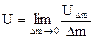
(предполагается, что такой предел существует). Аналогично введем элементарные притоки внешних энергий к единице массы среды
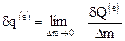 ,
, 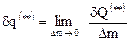 .
.
Разделив (12.3) на 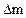 и устремив
и устремив 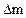 к нулю, запишем дифференциальное уравнение притока тепла в виде
к нулю, запишем дифференциальное уравнение притока тепла в виде
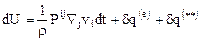 , (12.4)
, (12.4)
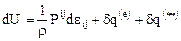 . (12.5)
. (12.5)
Лекция 13
Второй закон термодинамики. Уравнение для энтропии.
Второй закон утверждает, что невозможно устройство, которое переводило бы тепло от тела с меньшей температурой к телу с большей температурой без каких-либо изменений в других телах. Т.е. второй закон термодинамики характеризует направленность термодинамических процессов.
Обобщенная количественная формулировка второго закона сводится к утверждению существования функции состояния энтропии 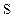 и абсолютной температуры
и абсолютной температуры 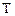 таких, что для произвольных вообще необратимых процессов имеет место равенство
таких, что для произвольных вообще необратимых процессов имеет место равенство
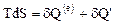 ,
,
где 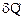 - так называемое некомпенсированное тепло. По определению принимается, что
- так называемое некомпенсированное тепло. По определению принимается, что 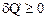 , причем знак равенства имеет место для обратимых процессов, а неравенство – для обратимых.
, причем знак равенства имеет место для обратимых процессов, а неравенство – для обратимых.
В случае обратимого процесса второй закон термодинамики имеет, таким образом, выражение
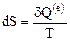 .
.
Фиксируя точку начального состояния системы  для любого состояния
для любого состояния  , в которое можно перейти из состояния обратимыми путями
, в которое можно перейти из состояния обратимыми путями
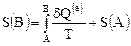 .
.
Если система теплоизолированная, но может подвергаться любым силовым воздействиям, то процессы, в которых она участвует, называются адиабатическими.
В этом случае внешний поток тепла к системе равен нулю 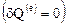 . В случае обратимых адиабатических процессов
. В случае обратимых адиабатических процессов
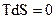 ,
,
поэтому
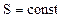 .
.
Обратимые адиабатические процессы являются изэнтропическими. Наоборот, если обратимый процесс изэнтропический, т.е. 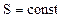 , то
, то 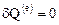 и процесс является адиабатическим.
и процесс является адиабатическим.
Если же процесс адиабатический и необратимый, то 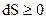 , и энтропия, если она изменяется, может только расти, так как
, и энтропия, если она изменяется, может только расти, так как 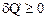 .
.
Лекция 14
Идеальная несжимаемая жидкость. Идеальный совершенный газ.
Вязкая несжимаемая жидкость.
В ряде случаев можно считать, что эффекты вязкости пренебрежимо малы. Для такой жидкости коэффициенты 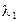 и
и 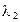 раны нулю и закон поведения среды принимает вид
раны нулю и закон поведения среды принимает вид
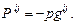 (14.1)
(14.1)
Жидкость с определяющим уравнением такого вида называется идеальной жидкостью.
Динамическое уравнение движения сплошной среды ввиду условия 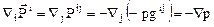 запишется для идеальной жидкости следующим образом.
запишется для идеальной жидкости следующим образом.
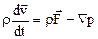 . (14.2)
. (14.2)
Последнее эквивалентно трем скалярным уравнениям Эйлера
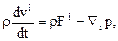 (14.3)
(14.3)
где
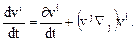
К этим уравнениям следует прибавить уравнение неразрывности в виде условия несжимаемости
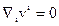 (14.4)
(14.4)
Система уравнений (14.3) и (14.4) является замкнутой и определяет модель идеальной несжимаемой жидкости.
В декартовой системе координат система уравнений (14.3) и (14.4) имеет вид
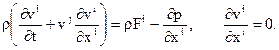
Примером модели идеальной сжимаемой жидкости может служить модель идеального совершенного газа, которую задают обычно двумя функциями:
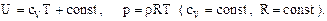 (14.5)
(14.5)
В этом случае, если массовые силы 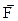 и внешний приток тепла
и внешний приток тепла 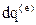 заданы, то уравнение притока тепла
заданы, то уравнение притока тепла
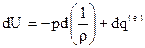 , (14.6)
, (14.6)
уравнение неразрывности (14.4) и три уравнение движения Эйлера (14.3) представляют собой замкнутую систему для определения шести неизвестных скалярных функций 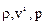 и
и 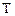 .
.
Количество тепла, поступающее к единице массы среды 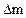 за время
за время 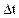 , равно
, равно
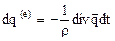 , (14.7)
, (14.7)
где вектор 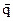 называется вектором потока тепла. Поток тепла
называется вектором потока тепла. Поток тепла 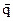 для большинства изотропных сред связан с полем температуры
для большинства изотропных сред связан с полем температуры 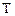 законом Фурье
законом Фурье
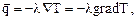 (14.8)
(14.8)
где l - коэффициент теплопроводности является функцией температуры 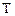 . практически очень важный простой случай, когда l=const. Тогда, для притока тепла
. практически очень важный простой случай, когда l=const. Тогда, для притока тепла 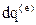 на единицу массы газа, из формулы (6.13) на основе (6.14) получим
на единицу массы газа, из формулы (6.13) на основе (6.14) получим
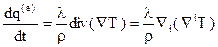
или
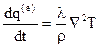 ,
,
где 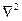 - оператор Лапласа.
- оператор Лапласа.
Таким образом, уравнение притока тепла для идеального совершенного газа в том случае, когда приток тепла обусловлен теплопроводностью по закону Фурье и 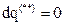 , будет иметь вид
, будет иметь вид
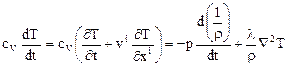 . (14.9)
. (14.9)
Рассмотрим изотермические движение однородной вязкой несжимаемой жидкости. Следствием требования несжимаемости и однородности является постоянство плотности жидкости
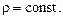
Жидкость вязкая, если тензор напряжений связан с тензором скоростей деформаций законом Навье-Стокса. Следовательно, поверхностная сила, кроме нормальной имеет еще и касательную составляющую.
Для изотермических процессов можно принять, что коэффициенты вязкости имеют постоянные значения. С учетом этого и условия несжимаемость 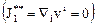 следует
следует
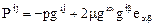 ,
,
где
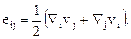
Таким образом
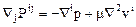
или в векторной форме
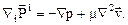
Уравнения движения среды в рассматриваемом случае принимают вид
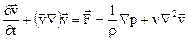 (14.10)
(14.10)
или
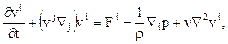
где 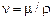 - кинематический коэффициент вязкости
- кинематический коэффициент вязкости
Уравнение (14.10) называют уравнением Навье-Стокса.
Присоединим еще уравнение неразрывности (14.4) и получаем замкнутую систему уравнений для определения трех компонент скоростей и давления, т.е.
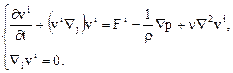 (14.11)
(14.11)
 2021-12-25
2021-12-25 131
131








