Решение второй задачи динамики иногда удается упростить с помощью общих теорем динамики точки: теоремы об изменении количества движения, теоремы об изменении момента количества движения и теоремы об измене-нии кинетической энергии.
Основное равенство динамики для материальной точки с постоянной массой можно представить в виде
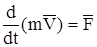 ;
;
или
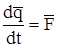 ; (11.8)
; (11.8)
где 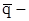 вектор количества движения материальной точки
вектор количества движения материальной точки
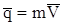 .
.
Термин «количество движения» был использован Ньютоном в формулировке своего 2-го закона: «изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует».
Переписывая равенство (11.8) в форме
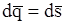 ; (11.9)
; (11.9)
где 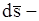 элементарный импульс силы
элементарный импульс силы 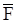
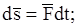
получим аналитическое выражение теоремы об изменении количества дви-жения материальной точки, которая гласит, что дифференциал количества движения материальной точки равен элементарному импульсу действующей на точку силы.
Равенство (11.9) выражает дифференциальную форму теоремы об изменении количества движения материальной точки. Если рассматривать движение точки на конечном промежутке времени от момента времени 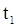 , когда скорость точки была равна
, когда скорость точки была равна 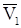 , до момента времени
, до момента времени 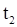 , когда скорость
, когда скорость
точки равна 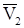 , то теорему можно представить в интегральной форме
, то теорему можно представить в интегральной форме
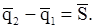 (11.10)
(11.10)
Здесь 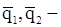 количество движения точки в моменты времени
количество движения точки в моменты времени 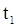 и
и 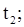
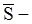 пол-ный импульс действующей на точку силы
пол-ный импульс действующей на точку силы 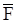 за промежуток времени
за промежуток времени 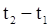
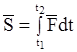 .
.
Таким образом, согласно равенству (11.10) изменение количества движения материальной точки за конечный промежуток времени равно полному импульсу силы, действующей на точку за тот же промежуток времени.
Если 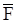 = 0, то согласно равенству (11.8) вектор количества движения точки является постоянной величиной
= 0, то согласно равенству (11.8) вектор количества движения точки является постоянной величиной
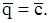
Это равенство выражает закон сохранения количества движения точки. Точка движется со скоростью, постоянной по модулю и направлению. Зависимости
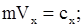
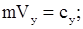
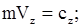
называются первыми интегралами уравнений движения точки.
Если 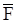 параллельна оси OZ, то
параллельна оси OZ, то 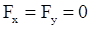 , что соответствует двум первым интегралам уравнений движения точки
, что соответствует двум первым интегралам уравнений движения точки
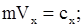
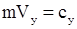 .
.
Отсюда
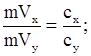
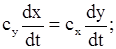
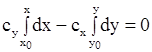 .
.
В результате получаем уравнение плоскости параллельной оси Z, в которой движется точка

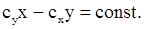
Когда 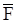 перпендикулярна оси OX, то есть когда
перпендикулярна оси OX, то есть когда 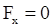 , можно запи-сать один первый интеграл
, можно запи-сать один первый интеграл
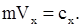
11.5. Теорема об изменении момента количества движения точки.
Левую и правую части основного равенства динамики (11.1) умножим векторно на радиус-вектор  , определяющий положение материальной точки относительно некоторого центра О
, определяющий положение материальной точки относительно некоторого центра О
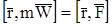 . (11.11)
. (11.11)
Представим левую часть этого равенства в виде
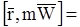
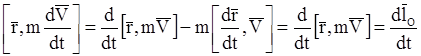 .
.
Здесь  вектор момента количества движения материальной точки относи-тельно центра О
вектор момента количества движения материальной точки относи-тельно центра О

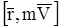 .
.
Векторное произведение, расположенное в правой части равенства (11.11), определяет момент силы 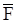 , взятый относительно центра О
, взятый относительно центра О
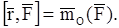
В результате вместо равенства (11.11) получаем аналитическое выражение теоремы об изменении момента количества движения материальной точки в
дифференциальной форме
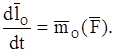 (11.12)
(11.12)
Согласно теореме скорость изменения момента количества движения мате-риальной точки относительно некоторого центра О равна моменту действу-ющей на точку силы, взятому относительно того же центра О.
В случае, когда рассматривается движение точки на конечном проме-жутке времени, используется интегральная форма теоремы, получаемая в результате интегрирования уравнения (11.12).
При 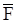 = 0 из уравнения (11.12) следует, что
= 0 из уравнения (11.12) следует, что
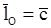 . (11.13)
. (11.13)
Равенство (11.13), выражающее закон сохранения момента количества дви-жения точки, позволяет записать три первых интеграла уравнений движения.
Учитывая, что

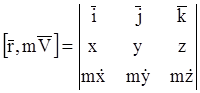 ; (11.14)
; (11.14)
будем иметь
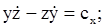
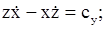
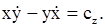
Такие же первые интегралы уравнений движения точки можно запи-сать, когда на точку действует центральная сила. Центральной силой называ-ется такая сила, линия действия которой в любой момент времени проходит через одну и ту же точку (центр) пространства. В случае центральной силы
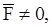 но
но 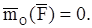 Поэтому
Поэтому 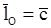 .
.
Если 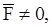 но
но 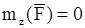 , то есть когда линия действия силы
, то есть когда линия действия силы 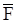 параллельна или пересекает ось OZ, можно записать один первый интеграл уравнений движения точки
параллельна или пересекает ось OZ, можно записать один первый интеграл уравнений движения точки
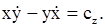
 2021-07-31
2021-07-31 85
85








