Если на материальную точку действуют только потенциальные силы, то теорему об изменении кинетической энергии можно записать в виде
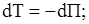
или
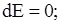 (11.22)
(11.22)
где 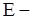 полная механическая энергия материальной точки
полная механическая энергия материальной точки
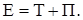
Из равенства (11.22) следует первый интеграл уравнений движения точки, называемый интегралом энергии
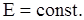
Интеграл энергии выражает закон сохранения полной механической энергии материальной точки, согласно которому при движении точки под действием потенциальных сил ее полная механическая энергия остается постоянной.
Силовое поле, в котором соблюдается закон сохранения полной меха-нической энергии, называется консервативным. Консервативное силовое по-ле – это идеализация силовых полей, у которых рассеиванием энергии можно пренебречь. В случаях, когда рассеивание энергии при движении точки необ-ходимо учитывать, теорема об изменении кинетической энергии переписы-вается таким образом
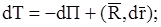 (11.23)
(11.23)
где 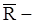 диссипативная (рассеивающая) сила.
диссипативная (рассеивающая) сила.
Например, если
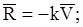
то
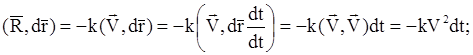
и вместо равенства (11.23) получим следующее
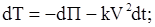
или
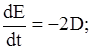
где 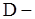 диссипативная функция
диссипативная функция
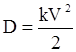 .
.
При 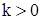 функция D > 0 и полная механическая энергия материальной точки, которая движется под действием диссипативных сил (сил трения, сопротивления среды), убывает.
функция D > 0 и полная механическая энергия материальной точки, которая движется под действием диссипативных сил (сил трения, сопротивления среды), убывает.
11.8. Прямолинейное движение точки.
Применение теорем динамики точки при решении второй (основной) задачи динамики поясним на конкретных примерах.
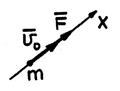 Рассмотрим прямолинейное движение материальной точки, которое происходит под действием постоянной по направлению силы
Рассмотрим прямолинейное движение материальной точки, которое происходит под действием постоянной по направлению силы 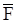 с начальной скоростью
с начальной скоростью 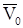 , направленной вдоль вектора
, направленной вдоль вектора 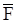 (рис. 11.6).
(рис. 11.6).
Движение точки описывается следующим дифференциаль-ным уравнением
Рис. 11.6. 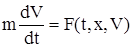 . (11.24)
. (11.24)
В общем случае для определения скорости и закона движения уравнение (11.24) интегрируется известными аналитическими или численными метода-ми. Однако, в частных случаях, которые рассматриваются ниже, решение задачи можно упростить.
Допустим, что действующая на материальную точку сила зависит толь-ко от времени. Тогда с помощью интегральной формы теоремы об изменении количества движения точки можно записать
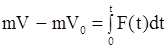 .
.
Отсюда находим
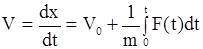 ;
; 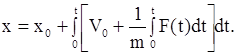
Если действующая на материальную точку сила зависит только от координаты, то на основании теоремы об изменении кинетической энергии
записываем
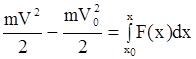 .
.
Решая это уравнение, получим выражения для скорости точки и закона ее движения
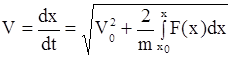 ;
;
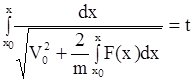 .
.
 2021-07-31
2021-07-31 391
391








