11.2. Дифференциальные уравнения движения материальной точки.
Если принять во внимание, что
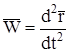 ;
;
где  радиус-вектор точки, то равенство (11.1) можно представить в виде дифференциального уравнения
радиус-вектор точки, то равенство (11.1) можно представить в виде дифференциального уравнения
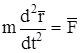 . (11.2)
. (11.2)
При задании движения точки в декартовых координатах векторное уравнение (11.2) заменяется системой скалярных уравнений
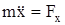 ;
; 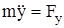 ;
; 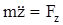 ; (11.3)
; (11.3)
где 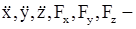 проекции векторов ускорения точки
проекции векторов ускорения точки 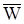 и силы
и силы 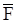 на оси декартовой системы координат.
на оси декартовой системы координат.
Если движение точки задано в естественных осях, то с учетом выражений, определяющих проекции ускорения точки при задании движения естест-венным способом, вместо векторного уравнения (11.2) будем иметь
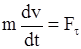 ;
; 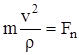 ;
;
где 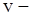 скорость точки;
скорость точки; 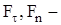 проекции вектора силы
проекции вектора силы 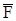 , направленные вдоль векторов
, направленные вдоль векторов 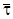 и
и 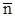 ;
; 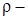 радиус кривизны траектории точки.
радиус кривизны траектории точки.
В полярных координатах 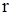 и
и 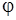 движение точки описывается системой
движение точки описывается системой
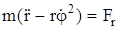 ;
; 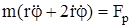 ;
;
где  проекции вектора силы
проекции вектора силы 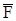 на радиальное и трансверсальное
на радиальное и трансверсальное
направления.
11.3. Две задачи динамики.
Рассмотрим решение первой и второй задач динамики при задании движения точки в декартовых координатах.
Если принять во внимание, что в общем случае
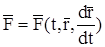 ;
;
то система (11.3) переписывается в виде
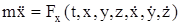 ;
;
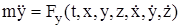 ;
;
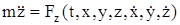 . (11.4)
. (11.4)
В первой задаче динамики требуется найти действующую на точку силу F по известным зависимостям 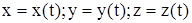 . Как следует из уравнений (11.4) для определения проекций силы F достаточно дважды продифференцировать заданные зависимости по времени, а затем по полу-ченным значениям
. Как следует из уравнений (11.4) для определения проекций силы F достаточно дважды продифференцировать заданные зависимости по времени, а затем по полу-ченным значениям 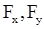 и
и 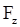 подсчитать модуль искомой силы
подсчитать модуль искомой силы
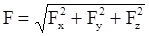 .
.
Во второй задаче по заданным проекциям силы, действующей на мате-риальную точку, требуется определить ее движение. То есть вторая задача динамики сводится к решению системы дифференциальных уравнений (11.4) с известными функциями 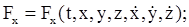
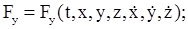 и
и
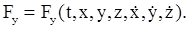 Следует отметить, что для такой системы не всегда удается получить точное аналитическое решение. В подобных случаях приходится обращаться к приближенным аналитическим методам или численному интегрированию.
Следует отметить, что для такой системы не всегда удается получить точное аналитическое решение. В подобных случаях приходится обращаться к приближенным аналитическим методам или численному интегрированию.
Если систему удалось проинтегрировать и получить общее решение в виде
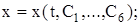
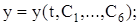
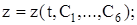 (11.5)
(11.5)
где 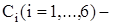 постоянные интегрирования, то после его дифференциро-вания по времени, получим
постоянные интегрирования, то после его дифференциро-вания по времени, получим
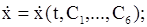
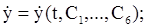
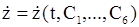 . (11.6)
. (11.6)
Равенства вида (11.6) получили название первых интегралов уравнений движения. Подстановка в равенства (11.5), (11.6) заданных в условии задачи начальных условий (при t = 0: 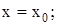
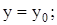
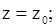
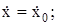
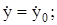
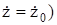 позволяет найти зависимости постоянных интегрирования от начальных условий
позволяет найти зависимости постоянных интегрирования от начальных условий
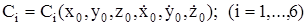 .
.
Подставив полученные значения 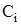 в общее решение (11.5), получим иско-мое решение задачи
в общее решение (11.5), получим иско-мое решение задачи

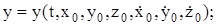
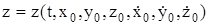 .
.
Пример 11.1. Точка массы 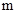 движется с начальной скоростью
движется с начальной скоростью 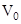 по эллипсу
по эллипсу
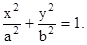
Ускорение точки параллельно оси OY. При t = 0: 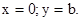 Требуется определить действующую на точку силу
Требуется определить действующую на точку силу 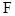 .
.
Движение точки в плоскости XOY описывается следующей системой уравнений
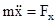 ;
; 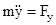 .
.
В данном случае известно, что ускорение точки параллельно оси OY. Это означает, что
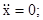 и, следовательно,
и, следовательно, 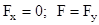 ;
; 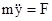 .
.
Из уравнения, описывающего траекторию точки, находим
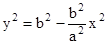 ;
; 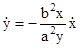 .
.
Так как 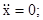
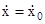 . При t = 0:
. При t = 0: 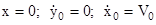 . Следовательно
. Следовательно
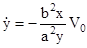 ;
; 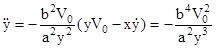 ;
; 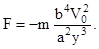
Пример 11.2. Материальная точка начинает движение из состояния покоя под действием силы тяжести 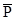 и силы сопротивления среды, пропорциональной первой степени скорости:
и силы сопротивления среды, пропорциональной первой степени скорости: 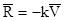 . Требуется найти скорость и записать уравнение движения точки.
. Требуется найти скорость и записать уравнение движения точки.
Основное равенство динамики (11.1) в данном случае записывается в виде
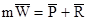 .
.
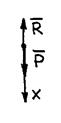 Спроектируем это равенство на ось ОХ, направленную вдоль прямолинейной траектории движения точки (рис. 11.1)
Спроектируем это равенство на ось ОХ, направленную вдоль прямолинейной траектории движения точки (рис. 11.1)
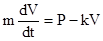 . (11.7)
. (11.7)
Рис. 11.1. Уравнение (11.7) – дифференциальное уравнение первого порядка. Разделяя
переменные и интегрируя в пределах, заданных условием задачи, находим
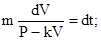
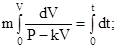
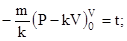
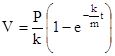 .
.
Чтобы записать уравнение движения точки, полученную зависимость скорости V от времени t представим дифференциальным уравнением
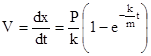 .
.
Разделяя переменные и интегрируя, получим
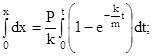
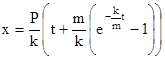 .
.
 2021-07-31
2021-07-31 666
666








