Задача 2-х тел

В предыдущем разделе рассматривалось движение планеты относительно притягивающего планету неподвижного Солнца. Но в действительности происходит взаимное притяжение Солнца и движущейся вокруг него планеты. Задача, в которой планета и Солнце испытывают взаимное притяжение, получила название задачи 2-х тел.

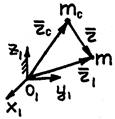    Допустим, что планета и Солнце движутся относительно неподвижной системы координат 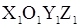. Положение планеты и Солнца относительно начала определяют радиус-векторы 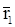 и 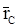, а положение планеты относительно Солнца – радиус-вектор  (рис. 11.8).

 Движения планеты и Солнца относительно системы 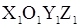 описываются следующими уравнениями

Рис. 11.8.

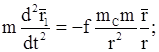                                                                        (11.34)

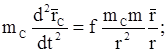                                                                                               (11.35)

Умножим левые и правые части уравнений (11.34) и (11.35) на 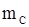 и 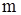, соответственно, и из первого полученного таким образом выражения вычтем второе. В результате будем иметь     

.

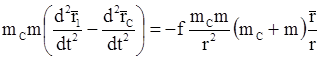Учитывая, что

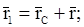
окончательно получим

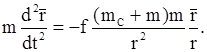                                                                        (11.36)

Из равенства (11.36) видно, что задача о движении планеты и Солнца под действием сил взаимного притяжения сводится к задаче о движении планеты вокруг Солнца как вокруг неподвижного притягивающего центра, в котором сосредоточена масса, равная сумме масс Солнца и планеты.

Отсюда следует, что при учете взаимного притяжения планеты и Солнца постоянная Гаусса 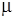 может считаться постоянной для всех планет Солнечной системы только приближенно, когда 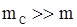. Соответствующие поправки необходимо внести и в 3-ий закон Кеплера. Так, для планет с массам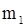и  и 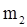 можно записать

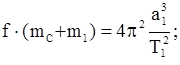
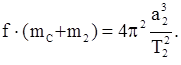
Отсюда находим

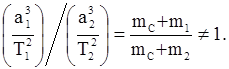
Это означает, что 3-ий закон Кеплера также имеет приближенный характер. Его можно считать справедливым, если масса планеты пренебрежимо мала в сравнении с массой Солнца.

    Таким образом, задача 2-х тел сводится к задаче о движении одного тела (планеты), которое движется вокруг неподвижного центра (Солнца) под действием его сил притяжения. Для многих подобных задач находятся точные аналитические решения. Иначе обстоит дело, когда рассматривается движение n тел, испытывающих взаимное притяжение. Даже в задаче с тремя телами (задача 3-х тел) точные решения удается получить только в нескольких специальных случаях. В общем случае при произвольных начальных скоростях и координатах движущихся тел решения задачи 3-х тел в виде конечных аналитических выражений не существует.